whereitsbeen
- 6
- 0
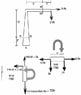
Calculate the internal reactions for the member shown at the sections indicated;
picture attached with FBD's
I have the V & F forces correct but my moments are off. Can you point me in the right direction here?
V M-M = 2k
F M-M =-0.5k
V N-N = -2k
F N-N = 0.5k
M M-M = -10k (2) + 0.5k (2) + 2k -0.5k + M=0
M= -18.5 k/ft
answer claims to be 21k/ft
M N-N = -2k (3) + 0.5k (3) - 2k +0.5k +M=0
M= - 6 k/ft
answer claims to be + 6k/ft
Thank You
-Mike
picture attached with FBD's
I have the V & F forces correct but my moments are off. Can you point me in the right direction here?
V M-M = 2k
F M-M =-0.5k
V N-N = -2k
F N-N = 0.5k
M M-M = -10k (2) + 0.5k (2) + 2k -0.5k + M=0
M= -18.5 k/ft
answer claims to be 21k/ft
M N-N = -2k (3) + 0.5k (3) - 2k +0.5k +M=0
M= - 6 k/ft
answer claims to be + 6k/ft
Thank You
-Mike