GingerBread27
- 108
- 0
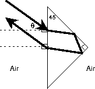
A corner reflector is to be made from a triangular prism with index of refraction n=2.56, as shown in the diagram on your assignment. What is the maximum angle (in °), with respect to the normal to the front surface of the prism, (theta), such that total reflection will occur?
Ok this must be easy since it is one of the first problems in my assignment , but I'm not getting it, any ideas?
Ok this must be easy since it is one of the first problems in my assignment , but I'm not getting it, any ideas?