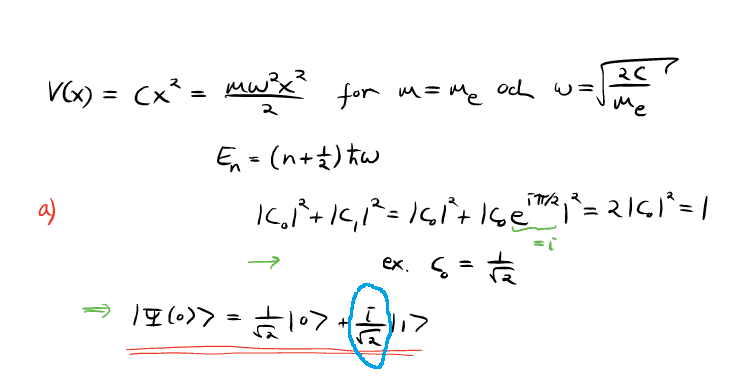SUMMARY
The discussion focuses on the normalization of the quantum state coefficient c1, specifically addressing the relationship c1 = i c0, which introduces the complex number i into the normalization process. Participants clarify that the normalization yields i/sqrt(2) due to the absolute value squared of the complex number. The exponential form e^(iπ/2) is also discussed, illustrating the connection between complex numbers and quantum mechanics. This highlights the necessity of understanding complex coefficients in quantum state normalization.
PREREQUISITES
- Understanding of complex numbers in mathematics
- Familiarity with quantum mechanics terminology
- Knowledge of normalization in quantum states
- Basic grasp of Euler's formula e^(ix) = cos(x) + i sin(x)
NEXT STEPS
- Study the implications of complex coefficients in quantum mechanics
- Learn about quantum state normalization techniques
- Explore Euler's formula and its applications in physics
- Investigate the role of complex numbers in wave functions
USEFUL FOR
Students and professionals in physics, particularly those studying quantum mechanics, as well as mathematicians interested in the application of complex numbers in physical theories.