- #1
OneLastTry
- 3
- 0
I recently did an experiment to measure the activity of a radioactive source, with the idea that the activity can be found by treating the detector area as part of the surface area of a sphere.
In the actual experiment, we plotted
[tex] u = \frac{n d^2}{\Delta t} [/tex]
against d, where d is the distance between the source and detector, [tex]\Delta t[/tex] is the time over which the measurement was taken, and n was the number of counts recorded. The point of this was that if the inverse square law was obeyed, u would be approximately constant with any d (assuming the source was point-like, ignoring absorption of beta particles in air and detector dead time).
The plot of the data looked more like an arctan graph, which made sense when setting the problem up geometrically:
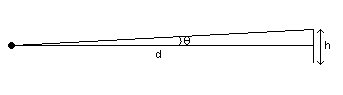
With a detector of height h, distance d from the source, any particles emitted in one dimension with an angle less than
[tex]\theta = 2 \arctan{\left(\frac{h}{2d}\right)}[/tex]
would strike the detector, and the same for the other dimension. If there is an equal probability of particle being emitted from any angle, then the fraction hitting the detector is
[tex]\left(\frac{\theta}{2 \pi}\right)^2[/tex]
(possibly with a factor of 1/2, I wasn't sure if the second dimension should use [tex]\theta / 2 \pi[/tex] or [tex]\theta / \pi[/tex], as in spherical polars), so
[tex]u = \frac{N d^2}{\Delta t} \left(\frac{2 \arctan{\left(\frac{h}{2d}\right)}}{2 \pi}\right)^2[/tex],
where N is the activity of the source.
When I showed this to my demonstrator, he told me I was talking bollocks and that any deviation from the expected inverse-square fit was because the source was line-like rather than point-like. I argued that because the detector is flat rather than curved as though on the surface of a sphere you wouldn't see an inverse-square fit even with a point source, but he was pretty adamant.
Am I in fact talking bollocks, or does my argument make sense?
In the actual experiment, we plotted
[tex] u = \frac{n d^2}{\Delta t} [/tex]
against d, where d is the distance between the source and detector, [tex]\Delta t[/tex] is the time over which the measurement was taken, and n was the number of counts recorded. The point of this was that if the inverse square law was obeyed, u would be approximately constant with any d (assuming the source was point-like, ignoring absorption of beta particles in air and detector dead time).
The plot of the data looked more like an arctan graph, which made sense when setting the problem up geometrically:
With a detector of height h, distance d from the source, any particles emitted in one dimension with an angle less than
[tex]\theta = 2 \arctan{\left(\frac{h}{2d}\right)}[/tex]
would strike the detector, and the same for the other dimension. If there is an equal probability of particle being emitted from any angle, then the fraction hitting the detector is
[tex]\left(\frac{\theta}{2 \pi}\right)^2[/tex]
(possibly with a factor of 1/2, I wasn't sure if the second dimension should use [tex]\theta / 2 \pi[/tex] or [tex]\theta / \pi[/tex], as in spherical polars), so
[tex]u = \frac{N d^2}{\Delta t} \left(\frac{2 \arctan{\left(\frac{h}{2d}\right)}}{2 \pi}\right)^2[/tex],
where N is the activity of the source.
When I showed this to my demonstrator, he told me I was talking bollocks and that any deviation from the expected inverse-square fit was because the source was line-like rather than point-like. I argued that because the detector is flat rather than curved as though on the surface of a sphere you wouldn't see an inverse-square fit even with a point source, but he was pretty adamant.
Am I in fact talking bollocks, or does my argument make sense?