Irregular sculpture hanging from two thin vertical wires

[guille1]

i have been stuck on this question for two days, can anyone help!

A museum of modern art is displaying an irregular 358 N sculpture by hanging it from two thin vertical wires, A and B, that are 1.25 m apart . The center of gravity of this piece of art is located 48.0 cm from its extreme right tip.

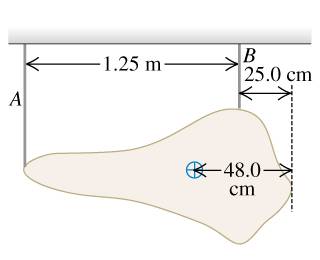
Find the tension in the wire A.

Find the tension in the wire B.

 

[berkeman]

Two days? Show us the FBDs you've drawn during this period of work...

 

[Gyro]

I think it's like you have to say that since the object is in equilibrium, there are no external unbalanced forces or torques acting on the system. That means F=ma in the vertical direction (up is +ve) gives you Ta + Tb = << edited out by berkeman >> . Then, assigning counter-clockwise as +ve and using the center of gravity as the point about which to sum moments, you have Tau(net) = 0 = << edited out by berkeman >> . Now we have two equations and two unknowns. Not hard to solve from there. I think that's how you do it, but I'm still learning too, so I'm not sure. :shy: Just trying to help out as much I can.

 

[berkeman]

I think it's like you have to say that since the object is in equilibrium, there are no external unbalanced forces or torques acting on the system. That means F=ma in the vertical direction (up is +ve) gives you Ta + Tb = << edited out by berkeman >> . Then, assigning counter-clockwise as +ve and using the center of gravity as the point about which to sum moments, you have Tau(net) = 0 = << edited out by berkeman >> . Now we have two equations and two unknowns. Not hard to solve from there. I think that's how you do it, but I'm still learning too, so I'm not sure. :shy: Just trying to help out as much I can.

Thanks for the help, Gyro. Please remember to only provide hints on homework/coursework questions. We need to have the OP do the bulk of the work.

 

[Gyro]

I'm sorry about that. Won't happen again.

 

[berkeman]

I'm sorry about that. Won't happen again.

No worries. Even with the work deleted, you have still provided useful hints to the OP. Thanks.

 

[senorfux2u]

Is this set up correct?

TA + TB - mg = 0 = Ttot (since the object is in equilibrium)

Im not wure where to go from here or if this is even right