Is an epoch-based approach valid for modeling N-body systems?

[IDCS]

Consider a 3-body Newtonian system with equal masses such that velocity change at a given time epoch for a single body is given by:

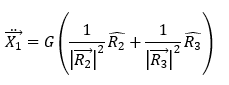
I am interpreting that if

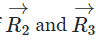also change per epoch such that say

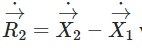which means

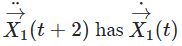as a component. So body state information propagates in a way that one could extrapolate this dynamic into a linear neural net to represent the entire system itself:

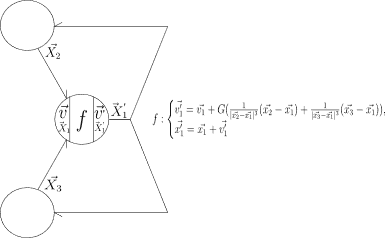
If such a shift in representation for such a fundamental problem was trivial like this, I would also expect to see it around more. So what am I missing here?

This is copying my post on https://physics.stackexchange.com/q...ed-approach-valid-for-modeling-n-body-systems

 

[Dale]

What you are calling “epoch based” is what is generally described as a numerical solution. The particular numerical solver you are describing is called Euler’s method. It is the simplest numerical differential equation solver and the first one taught in a numerical methods course. It is completely valid, but has some well known numerical instabilities, so in practice other methods are more commonly used.

 

[Filip Larsen]

Regarding the other methods Dale mentions, you may want to consider using a symplectic integrator that conserves mechanical system energy. An example of a symplectic integrator is the Verlet integrator which is almost just as easy to implement as explicit Euler.

Non-symplectic integrators, like the explicit Euler, will to a varying degree change the mechanical energy of the system which, in a pure N-body system, is supposed to be conserved thus giving rise to non-physical numerical solutions. For instance, simulating a 2-body bound system with explicit Euler will produce a slowly outward spiraling trajectory instead of a closed orbit as expected.

 

[IDCS]

Thank you for the answers. How about an Euler solver with sufficiently small time steps? I'd think something like Planck time would fit real world models with the speed of information travel and all that.

edit: To provide context, I am studying systems emergence and started my current most recent project on social opinion dynamics actually, so excuse the informality with some terms given my background. So it would help me a lot if you could also expand on what contexts would one go for different solvers

 

[Dale]

How about an Euler solver with sufficiently small time steps?

The Euler method is a first order method meaning that the numerical errors scale with the step size. Meaning that if you half your step size then you will half your error.

Probably the most popular Euler-like method it the Runge Kutta 4 method. That is a fourth order method, so if you half your step size your error will be 1/16 of the original error.

I'd think something like Planck time would fit real world models with the speed of information travel and all that.

That would actually not be beneficial. If your step size is too small then you get numerical rounding errors.

 

[IDCS]

That would actually not be beneficial. If your step size is too small then you get numerical rounding errors.

I mean in a simulation context where it can be assigned any standard value, not for computing real life systems.

 

[Filip Larsen]

How about an Euler solver with sufficiently small time steps?

Euler is a first order method so global truncation error for a solution can be expected to scale linearly with step size. However, the work involved in producing a global solution and rounding error scales inversely with step size so there is a practical lower limit to the step size before the global error starts to increase again.

In short, explicit Euler is about the integrator with worst overall performance for many types of problems for a given solution accuracy. When comparing the computation effort involved in producing a solution with a given global error (truncation and rounding) it is quite common that higher order methods win even though they may have far more evaluations of the field (per step).

Of course, if you do not require your solutions to be accurate at all (for example, if its purpose is an "artistic" animation of planet and you don't care about conservation of mechanical system energy) then the explicit Euler may be what you want. But if you do require some level of accuracy I would still recommend that you look into higher order symplectic methods like the mentioned Verlet method (which really is quite easy to implement).

 

[Dale]

I mean in a simulation context where it can be assigned any standard value, not for computing real life systems.

Even in a simulation it would not be beneficial. Suppose I am doing something absurdly simple like using the Euler method to calculate the position as a function of time for a particle moving in 1 dimension at a constant velocity. So $x(0)=1$ and $v(t)=x’(t)=1$. Using Euler’s method we get $x(t+h)\approx x(t)+x’(t) * h$

So, for $h=1$ we get $x(1)=1+1*1=2$. That is perfect, no errors.

Now, what happens for $h=1.6 \ 10^{-35}$? We get $x(1.6 \ 10^{-35})=1+1*1.6 \ 10^{-35}$. That seems fine at first glance, but on my computer the machine precision is only about $2.2 \ 10^{-16}$. So this number is rounded off to 1. So we get $x(1.6 \ 10^{-35})=1$.

Because of roundoff error, we can’t even calculate the position of a particle moving at constant velocity, a calculation that has 0 truncation error.

 

[IDCS]

So, for $h=1$ we get $x(1)=1+1*1=2$. That is perfect, no errors.

Now, what happens for $h=1.6 \ 10^{-35}$? We get $x(1.6 \ 10^{-35})=1+1*1.6 \ 10^{-35}$. That seems fine at first glance, but on my computer the machine precision is only about $2.2 \ 10^{-16}$. So this number is rounded off to 1. So we get $x(1.6 \ 10^{-35})=1$.

What I was trying to see was what kind of issues can potentially arise when one decides to treat unit values like Planck units as integers. Say for instance, if one adopts a lattice model with unit time to be a single epoch and a unit length an arbitrary speed of information travel per epoch such that the change in object state reaches to other objects only in distance / unit length steps. One issue I see then is one would have to deal with fractional values for distance and time that were supposed to be unit values and the model would no longer be a lattice. Not to mention the bigger issue of model losing its realism by being classical at that scale.

 

[Dale]

what kind of issues can potentially arise when one decides to treat unit values like Planck units as integers

Well, the biggest issue is that we have no physics theories that work that way.

 

[IDCS]

Well, the biggest issue is that we have no physics theories that work that way.

How come? Lattice models are all the rage with the kids these days, one would think someone would formulate one for gravitational systems

 

[Dale]

How come?

Unfortunately, I don’t know the technical difficulties involved.

 

[Filip Larsen]

What I was trying to see was what kind of issues can potentially arise when one decides to treat unit values like Planck units as integers.

It is somewhat hazy to me what kind of theoretical or practical insight you are seeking, but if you are "just" talking about practical numerical issues in rescaling your problem so unit length and time is on the Planck scale, then, as also implied by Dale mentioning of precision, you need to use a numerical number library that allows you to represent and maintain the full precision you desire during calculations. Not that I think it would make any practical sense to solve an N-body problem with Planck scale precision.

I am not in position to comments on how much sense a lattice model would make on a theoretical level for an N-body solver, but for practical numerical work on big N-body problems it may make computational sense to use approximations that have some similarity with being lattice-like, like for instance octrees as used in Barnes-Hut simulation (I am only aware of this solver type, but do not have any practical experience with it).