AirForceOne
- 49
- 0
Hi,
Suppose I have this matrix A:
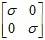
Why is the matrix exponential like so:
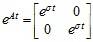
when A is not simple (eigenvalues not distinct)?
Thanks.
Suppose I have this matrix A:
Why is the matrix exponential like so:
when A is not simple (eigenvalues not distinct)?
Thanks.