Rolls With Slipping
- 11
- 6
- Homework Statement
- This is my own question I created to try and think about what would happen if two inductors with different currents are connected.
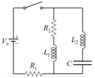
Assume the circuit elements all have non-zero values. The switch has been closed for a very long time such that the current through ## L_1 ## is constant and no current flows through ## L_2 ##. What will the current be through ## L_1 ## and ## L_2 ## after opening the switch?
- Relevant Equations
- ## V_L = L \frac{dI}{dt} ##
The standard assumption is that the current through an inductor must be continuous such that you don't produce an infinite back emf. However in this case, the current through ## L_1## is finite before opening the switch and the current through ## L_2 ## is zero before opening the switch. When the switch opens, is it possible for the current to be continuous through both?