Is it possible to have water levels at different heights without a pump?

[StefanBoon]

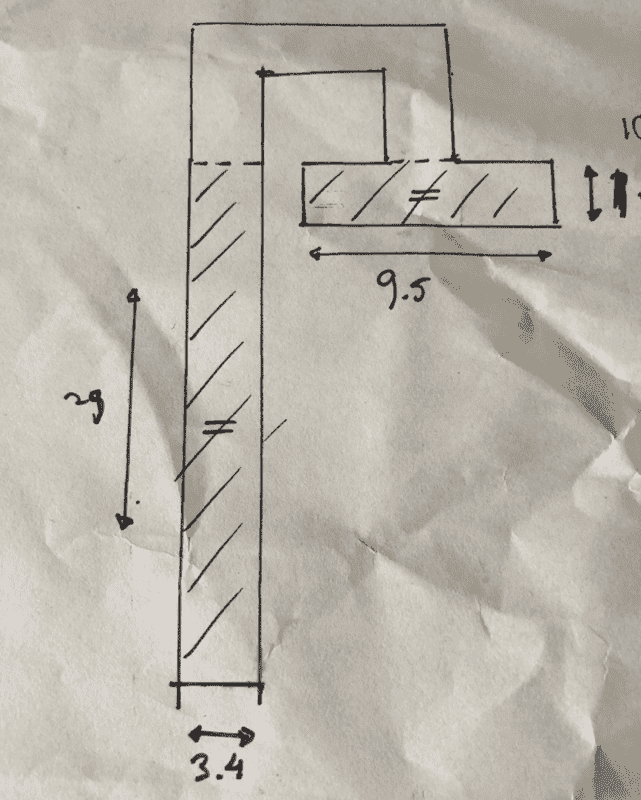
I wonder if air can remain trapped under a structure that has a deep and a shallow tube. I have already tested with a prototype whether increasing volume in the shallower tube works. Air bubbles came out on the short side, so this doesn't work. Is there any way to realize this concept.

 

[Nugatory]

The quick answer to your question is no, but it is worth spending some time thinking about why.

Think about the forces acting on the water right at the surface: if the downwards pressure from the air above is not exactly balanced by the upwards pressure from the water immediately underneath, the level will either fall (air pressure is greater) or rise (water pressure is greater). What can you say about the air and water pressures above the two tubes?

 

[StefanBoon]

The quick answer to your question is no, but it is worth spending some time thinking about why.

Think about the forces acting on the water right at the surface: if the downwards pressure from the air above is not exactly balanced by the upwards pressure from the water immediately underneath, the level will either fall (air pressure is greater) or rise (water pressure is greater). What can you say about the air and water pressures above the two tubes?

Thank you, very much appreciated. What do you mean with the last sentence 'What can you say about the air and water pressures above the two tubes?'

Do you mean that it can work if the pressures of the air above is the same as de water at the surface of the short tube?

 

[sophiecentaur]

I wonder if air can remain trapped under a structure that has a deep and a shallow tube.

First of all I have to point out a very basic fact that it is not the diameter of the pipe that affects pressure - just the height of the vertical column.

I'm not sure if the image is the exact layout where what you describe happens (or doesn't happen) It sounds as if you are describing what's known as an 'Air Lock'. In a situation where there is air in an inverted U, the 'bubble' of air can be longer than the differences in the two water levels. The section of trapped air floats and supports the water columns so you don't get a simple siphon effect. (Plumbers come across this problem all the time where there are long horizontal runs of pipe in low pressure systems.

Practical Note: your drawing shows a flat horizontal surface at the bottom of the upper section. This is not stable and one side or the other will fall after a very short time. You would need a free moving piston to keep that water surface flat and level. You need narrow tubes to make this work.