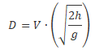- #1
DAB
- 6
- 0
I have seen this equation used to calculate the velocity of a projectile being launched off a table top.
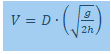 Where D=horizontal distance travelled, h=table height, and g=gravitational acceleration. Nowhere else can I find a calculation of velocity based on only two distances and GA. Everything I see has a time component or one of the velocity variables (V-i, V-f). Is this equation valid? It seems too simple. I don't care about exploring air resistance or drag coefficients, just a simple velocity at lauch calculation.
Where D=horizontal distance travelled, h=table height, and g=gravitational acceleration. Nowhere else can I find a calculation of velocity based on only two distances and GA. Everything I see has a time component or one of the velocity variables (V-i, V-f). Is this equation valid? It seems too simple. I don't care about exploring air resistance or drag coefficients, just a simple velocity at lauch calculation.