Is the Velocity of the Grapple Accurate Using Jacobian's Transformation?

[kinfo]

Hello!
I have some problems with geometry/kinematics, therefore i require in your help.
I need to estimate the velocity of manipulator's grapple.
I have found one solution (with the use of Jacobian's transformation), but i don't know, right it or wrong. Let's check together
Maybe existing is an easier one, or laconic etc.
Thx!
In order:
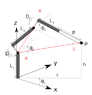
First step. Verification of the scheme. About the xyz axes. Why y-axis isn't perpendicular with z? What is a type of coordinate system?

 

[anorlunda]

Why y-axis isn't perpendicular with z?

Is is perpendicular. That drawing is the best you can do with 3 perpendicular axes depicted on 2D paper.

 

[kinfo]

Is is perpendicular. That drawing is the best you can do with 3 perpendicular axes depicted on 2D paper.

Thx. Great!
Then we can go forward)
Second step: estimate r and h.
h = L1+ L2*sinθ2+D1*cosθ2+(L3+d)*sin(θ2+θ3)+D2*sin(θ2+θ3)
r = L2*cosθ2 - D1*sinθ2+(L3+d)*cos(θ2+θ3)-D2*sin(θ2+θ3)
I don't understand, how it was deduced. Can you explain me on the aforementioned picture?
I must trace it by triangles? But how?
Thx.

 

[berkeman]

This is starting to sound like a schoolwork assignment...

 

[kinfo]

This is starting to sound like a schoolwork assignment...

No-no)
It is not schoolwork) I think, that schoolboys don't learn theoretical mechanics and Jacobian's transformation)))
I have a big problem with it, cause i have an other specialization (i can't know all )... but i must to do it(
So, can you help me with it?

Why:
h = L1+ L2*sinθ2+D1*cosθ2+(L3+d)*sin(θ2+θ3)+D2*sin(θ2+θ3)
r = L2*cosθ2 - D1*sinθ2+(L3+d)*cos(θ2+θ3)-D2*sin(θ2+θ3)?
How i must to trace the picture? Like this?

P.S. I have a full solution, but i want to understand.

 

[kinfo]

Sirs and Mesdames, no ideas too?