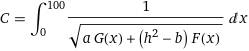SUMMARY
This discussion focuses on solving an integral with an unknown variable h using Python's SciPy library. The recommended approach involves defining a function f(h) that represents the difference between the integral and a constant C, and then utilizing SciPy's root solver to find the value of h that satisfies f(h) = 0. The integration is performed using scipy.integrate.quad_vec to simultaneously evaluate the function and its derivative, enhancing the efficiency of the solution process.
PREREQUISITES
- Understanding of integrals and their properties
- Familiarity with Python programming
- Knowledge of SciPy library functions, specifically
scipy.integrate.quad_vec and scipy.optimize
- Basic concepts of numerical methods, particularly Newton's method
NEXT STEPS
- Explore the documentation for
scipy.integrate.quad_vec to understand its usage and parameters
- Learn about root-finding algorithms in SciPy, focusing on
scipy.optimize.fsolve
- Study Newton's method in detail to grasp its application in numerical solutions
- Investigate error handling and validation techniques for numerical integration results
USEFUL FOR
Mathematicians, data scientists, and software developers who need to solve integrals with unknown variables using Python, particularly those utilizing the SciPy library for numerical computations.