Apashanka
- 427
- 15
- Homework Statement
- Requesting for re check
- Relevant Equations
- Requesting for re check
Problem Statement: Requesting for re check
Relevant Equations: Requesting for re check
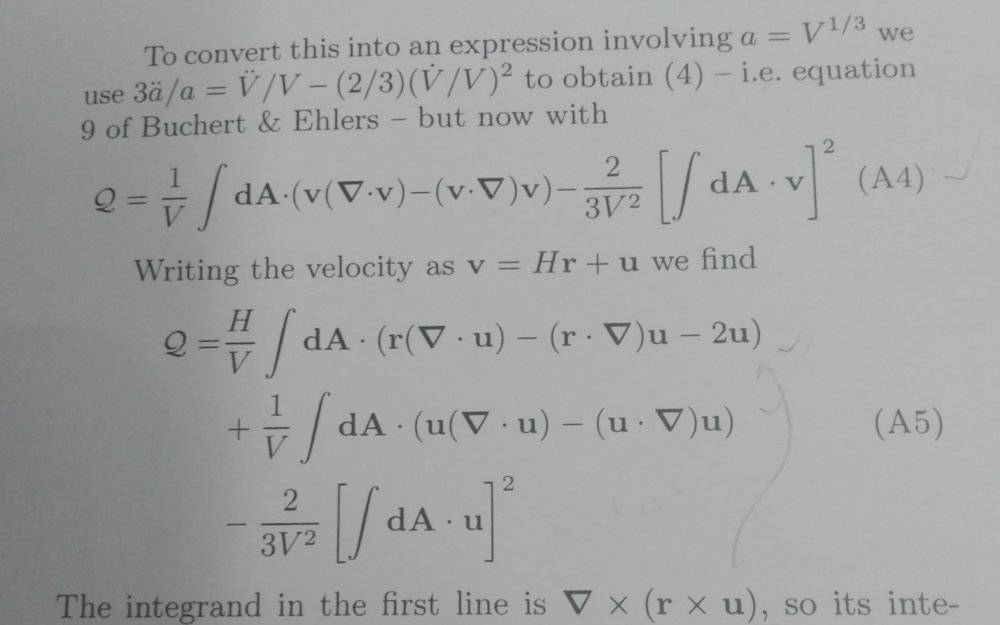
In this eq.A4 putting ##v=Hr+u## the first integrand in eq.A5 is coming as ##H(r(\nabla•u)-(r•\nabla)u+2u)\ne\nabla×(r×u)##
Am I right??
Can I request anyone to please recheck it...
using this the author has put the term ##\int_s(da•\nabla×(r×u))=0##(as closed surface) how then it is coming??
Will anyone please help...
##r## is the position vector and ##u ## is the peculiar velocity
Relevant Equations: Requesting for re check
In this eq.A4 putting ##v=Hr+u## the first integrand in eq.A5 is coming as ##H(r(\nabla•u)-(r•\nabla)u+2u)\ne\nabla×(r×u)##
Am I right??
Can I request anyone to please recheck it...
using this the author has put the term ##\int_s(da•\nabla×(r×u))=0##(as closed surface) how then it is coming??
Will anyone please help...
##r## is the position vector and ##u ## is the peculiar velocity
Last edited: