- #1
MatthijsRog
- 14
- 1
- TL;DR Summary
- Can I visualize intrinsic curvature without resorting to embeddibgs, by drawing a non-exhaustive set of geodesics on my space?
I’m working through the books by Schutz and Renteln to get my differential geometry to the point where I can do general relativity. The author’s have just introduced metrics and notions of parallel transport and with some work I finally understand how intrinsic curvature can be defined by watching parallel transport on loops.
Up until now, when I see authors defining n-dimensional manifolds, they visualize the curvature in such a manifold by embedding it into n+1-dimensional Euclidean space. Now there’s nothing wrong with this, but since doing GR is my goal I felt like visualizing everything as embeddings would be an impairment in the long run.
I figured I could perhaps use another method to visualize a n-dimensional curved space without resorting to embeddings. I figured I could just make a map of my surroundings and then draw a (arbitrary, non-exhaustive) set of geodesics on that map, to express a notion of curvature.
For instance, I could make a badly-drawn map of my bedroom in blue. Drawing geodesics in red, a visualization of a flat metric could be:
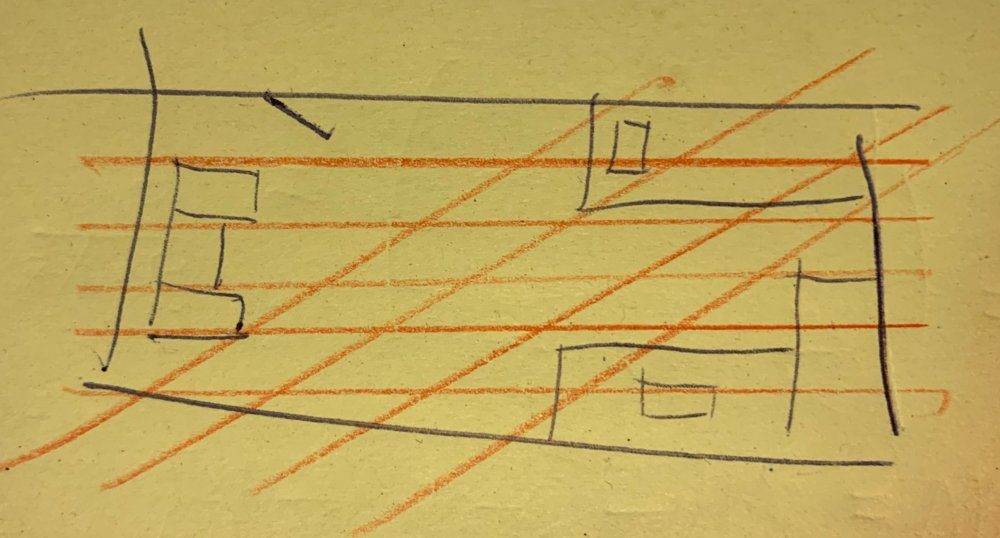
Should my bedroom for some weird, obscure reason become curved, I could depict the curved metric in an embedding, or keep the old blue map and draw new red geodesics on it:

The map isn't unique; I could've used other geodesics or kept the geodesics flat and warped the bedroom itself.
My question is: is this a good visualization method for curved metrics, that won't hurt me in the future? I'm asking this in the G.R. forums because I know there's a lot of bad G.R. visualization around, of which the heavy-ball-and-trampoline visualization is the prime example...I like my diagrams, but I wouldn't want to hurt my own learning curve by learning a bad visualization!
Up until now, when I see authors defining n-dimensional manifolds, they visualize the curvature in such a manifold by embedding it into n+1-dimensional Euclidean space. Now there’s nothing wrong with this, but since doing GR is my goal I felt like visualizing everything as embeddings would be an impairment in the long run.
I figured I could perhaps use another method to visualize a n-dimensional curved space without resorting to embeddings. I figured I could just make a map of my surroundings and then draw a (arbitrary, non-exhaustive) set of geodesics on that map, to express a notion of curvature.
For instance, I could make a badly-drawn map of my bedroom in blue. Drawing geodesics in red, a visualization of a flat metric could be:
Should my bedroom for some weird, obscure reason become curved, I could depict the curved metric in an embedding, or keep the old blue map and draw new red geodesics on it:
The map isn't unique; I could've used other geodesics or kept the geodesics flat and warped the bedroom itself.
My question is: is this a good visualization method for curved metrics, that won't hurt me in the future? I'm asking this in the G.R. forums because I know there's a lot of bad G.R. visualization around, of which the heavy-ball-and-trampoline visualization is the prime example...I like my diagrams, but I wouldn't want to hurt my own learning curve by learning a bad visualization!