trinot
- 2
- 0
Homework Statement
Chapter 15, Problem 26
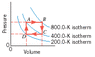
The drawing refers to 5.30 mol of a monatomic ideal gas and shows a process that has four steps, two isobaric (A to B, C to D) and two isochoric (B to C, D to A). (a) What is the work done from A to B? (b) What is the heat added or removed from B to C? (c) What is the change in internal energy from C to D? (d) What is the work done from D to A?
Homework Equations
W= nRT(Vf/Vi)
The Attempt at a Solution
W= 5.3mol * 8.31 * 800K *(Vf/Vi) this is where I am stick I don't know how to find the volume. I tried using V=nRT/P but I don't know the pressure?
Thanks in advance, the homework is due tonight.