Pax
- 3
- 1
There is this experiment my high school teacher showed in physics class. You are probably aware of it
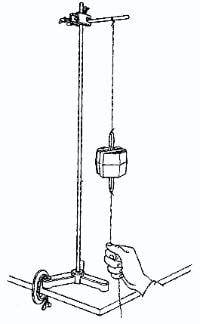 (from practicalphysics.org)
(from practicalphysics.org)
There is a video of a teacher actually doing the experiment here:
https://sites.google.com/site/haatscience/physics/221-the-effect-of-inertia
Gradually pull the thread and the top thread breaks, jerk the thread and the bottom one breaks.
I tried to set up a free body diagram to show how this works, and most specifically to solve for the rate of change of acceleration (jerk) that will be the threshold between the top string breaking and the bottom.
I am at a loss, how do you put dA/dt into the equations?
Any ideas?
There is a video of a teacher actually doing the experiment here:
https://sites.google.com/site/haatscience/physics/221-the-effect-of-inertia
Gradually pull the thread and the top thread breaks, jerk the thread and the bottom one breaks.
I tried to set up a free body diagram to show how this works, and most specifically to solve for the rate of change of acceleration (jerk) that will be the threshold between the top string breaking and the bottom.
I am at a loss, how do you put dA/dt into the equations?
Any ideas?
