CollegeStudent
- 109
- 0
1. Homework Statement
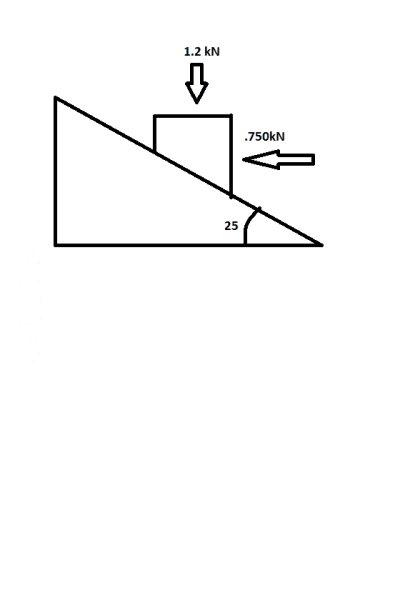
Determine whether the block shown is in equilibrium and find the magnitude and direction of the friction force when θ = 25° and P = 750N
μs[\SUB] = .35
μk[\SUB] = .25
2. Homework Equations
Fs = μs * N
Fk = μk * N
3. The Attempt at a Solution
Attachment 1 up there is the drawing of the scenario.
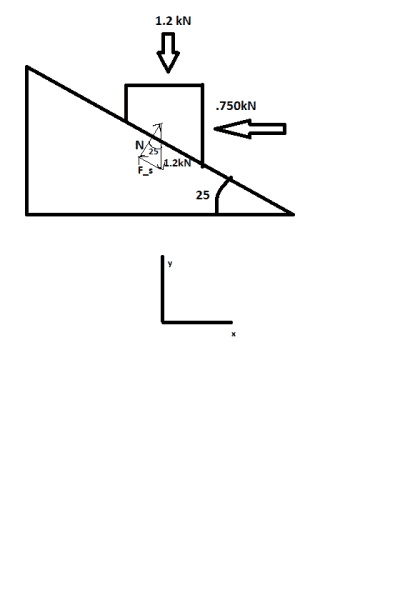
Attachment 2 is my addition to it to solve this problem.
Using the axis shown, I have
ΣFy = Ncosθ - Fssinθ - 1.2kN = 0
and apparently
ΣFx = Nsinθ - Fscosθ - .750kN = 0
otherwise that similar triangle I drew there wouldn't make sense, just odd to think of the force of friction acting in the SAME direction as the force...regardless, continuing...
Solving Top equation for Fs[\SUB] I get
Fs[\SUB] = (Ncosθ - 1.2kN)/(sinθ)
And subbing that into the second equation for F I receive
Nsinθ - ((Ncosθ - 1.2kN)/(sinθ))cosθ - .750 = 0
Nsinθ - (Ncos^2 θ - 1.2kNcosθ) - .750 = 0
N(sinθ - cos^2θ) + 1.2kNcosθ - .750 = 0
N = (-1.2kNcosθ + .750)/(sinθ - cos^2 θ)
N = 0.8465kN
So Fs[\SUB] = .35*0.8465kN = .2963kN
Seeing as how this doesn't match up to the answer given, I'm not seeing where I went off...can anyone guide me in the right direction? Should I use a slanted axis?
Determine whether the block shown is in equilibrium and find the magnitude and direction of the friction force when θ = 25° and P = 750N
μs[\SUB] = .35
μk[\SUB] = .25
2. Homework Equations
Fs = μs * N
Fk = μk * N
3. The Attempt at a Solution
Attachment 1 up there is the drawing of the scenario.
Attachment 2 is my addition to it to solve this problem.
Using the axis shown, I have
ΣFy = Ncosθ - Fssinθ - 1.2kN = 0
and apparently
ΣFx = Nsinθ - Fscosθ - .750kN = 0
otherwise that similar triangle I drew there wouldn't make sense, just odd to think of the force of friction acting in the SAME direction as the force...regardless, continuing...
Solving Top equation for Fs[\SUB] I get
Fs[\SUB] = (Ncosθ - 1.2kN)/(sinθ)
And subbing that into the second equation for F I receive
Nsinθ - ((Ncosθ - 1.2kN)/(sinθ))cosθ - .750 = 0
Nsinθ - (Ncos^2 θ - 1.2kNcosθ) - .750 = 0
N(sinθ - cos^2θ) + 1.2kNcosθ - .750 = 0
N = (-1.2kNcosθ + .750)/(sinθ - cos^2 θ)
N = 0.8465kN
So Fs[\SUB] = .35*0.8465kN = .2963kN
Seeing as how this doesn't match up to the answer given, I'm not seeing where I went off...can anyone guide me in the right direction? Should I use a slanted axis?
Last edited by a moderator: