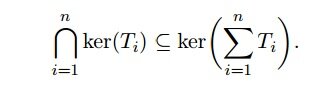You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
MHB Kernel on linear transformation proof
- Thread starter Cristian1
- Start date
Physics news on Phys.org
GJA
Gold Member
MHB
- 290
- 0
Hi Cristian,
If $$v\in \text{ker}(T_{1})\cap\text{ker}(T_{2}),$$
then what can we say about $$T_{1}(v)$$ and $$T_{2}(v)$$? With this question answered, we then look at
$$(T_{1}+T_{2})(v)=T_{1}(v)+T_{2}(v)=\ldots$$
I'm trying to give you a few hints so you can fill in the gaps on your own. Let me know if you're still confused/unclear on something.
If $$v\in \text{ker}(T_{1})\cap\text{ker}(T_{2}),$$
then what can we say about $$T_{1}(v)$$ and $$T_{2}(v)$$? With this question answered, we then look at
$$(T_{1}+T_{2})(v)=T_{1}(v)+T_{2}(v)=\ldots$$
I'm trying to give you a few hints so you can fill in the gaps on your own. Let me know if you're still confused/unclear on something.
Cristian1
- 3
- 0
thank you!
I see the point but don't see clearly the difference between the zero of the intersection and the zero of the sum
I see the point but don't see clearly the difference between the zero of the intersection and the zero of the sum
GJA
Gold Member
MHB
- 290
- 0
I will try to address what I think may be the confusion; if I have misunderstood you, just let me know.
My understanding of your question is that there is a perceived difference in the zero of the intersection and the zero of the sum. This is not the case: there is a single vector space, $$V,$$ and only one zero element of $$V.$$
What we are trying to show is ultimately set-theoretic in nature: we want to show that if an element $$v\in\bigcap_{i=1}^{n}\text{ker}(T_{i}),$$ then $$v\in \text{ker}\left(\sum_{i=1}^{n}T_{i} \right).$$ Let's break down what all this means:
To say that a vector belongs to the kernel of a linear transformation means that the linear transformation sends that vector to zero. So, by assuming $$v\in\bigcap_{i=1}^{n}\text{ker}(T_{i})$$ we are saying that $$v$$ makes all of the linear transformations zero; i.e.
$$T_{1}(v)=0,~ T_{2}(v)=0,\ldots, T_{n}(v)=0$$
In each case above the zero is the zero element of $$V,$$ they are not different zeros. Now, to show that $$v\in \text{ker}\left(\sum_{i=1}^{n}T_{i} \right),$$ we must show that when we plug $$v$$ into the function/linear transformation $$\sum_{i=1}^{n}T_{i}$$ we still get zero. For this we compute:
$$\left( \sum_{i=1}^{n}T_{i}\right)(v)=\sum_{i=1}^{n}T_{i}(v)=T_{1}(v)+T_{2}(v)+\ldots+T_{n}(v)=0+0+\ldots+0=0$$
Hence, $$v\in\text{ker}\left(\sum_{i=1}^{n}T_{i} \right).$$ Since $$v\in\bigcap_{i=1}^{n}\text{ker}(T_{i})$$ was arbitrary, the proof is finished.
Let's take an example to help us along. Let our vector space be
$$V=\mathbb{R}^{3}=\left\{\begin{bmatrix}x\\ y\\ z \end{bmatrix}: x, \, y, \, z\in\mathbb{R} \right\}$$
and our linear transformations $$T_{1}$$ & $$T_{2}$$ be given by
$$T_{1}\left(\begin{bmatrix}x\\y\\z \end{bmatrix} \right)=\begin{bmatrix}0\\y\\0 \end{bmatrix}$$
and
$$T_{2}\left(\begin{bmatrix}x\\y\\z \end{bmatrix} \right)=\begin{bmatrix}x\\0\\0 \end{bmatrix}$$
The zero element in this example is $$\begin{bmatrix}0\\0\\0\end{bmatrix}$$
Notice that $$T_{1}\left(\begin{bmatrix}x\\y\\z \end{bmatrix} \right)=\begin{bmatrix}0\\0\\0\end{bmatrix}$$
if and only if $$y=0.$$ Hence, $$\text{ker}(T_{1})=xz$$ plane. Similarly, $$\text{ker}(T_{2})=yz$$ plane. The intersection of these two kernels is the entire $$z$$ axis; i.e.
$$\bigcap_{i=1}^{2}\text{ker}(T_{i})=\left\{\begin{bmatrix}0\\0\\z \end{bmatrix}: z\in\mathbb{R} \right\}$$
(Drawing a picture of the two planes to see that their intersection is the $$z$$ axis may be helpful)
Now, if we wish to demonstrate the general proof you're working on in this example, we take an element $$\begin{bmatrix}0\\0\\z\end{bmatrix}\in \bigcap_{i=1}^{2}\text{ker}(T_{i})$$ and compute using the definitions of $$T_{1}$$ & $$T_{2}$$
$$\left(T_{1}+T_{2}\right)\left(\begin{bmatrix}0\\0\\z\end{bmatrix} \right)=T_{1}\left(\begin{bmatrix}0\\0\\z\end{bmatrix} \right)+T_{2}\left(\begin{bmatrix}0\\0\\z\end{bmatrix} \right)=\begin{bmatrix}0\\0\\0 \end{bmatrix} + \begin{bmatrix}0\\0\\0 \end{bmatrix} = \begin{bmatrix}0\\0\\0 \end{bmatrix}
$$
Hence, $$\begin{bmatrix}0\\0\\z\end{bmatrix}\in\text{ker}\left(\sum_{i=1}^{2}T_{i} \right)$$ as well. Thus, for this specific example,
$$\bigcap_{i=1}^{2}\text{ker}(T_{i})\subseteq \text{ker}\left(\sum_{i=1}^{2}T_{i} \right),$$
as it should be from your general exercise.
This is a long post, but I hope I have understood and addressed your concern. Let me know if anything is unclear/not quite right.
My understanding of your question is that there is a perceived difference in the zero of the intersection and the zero of the sum. This is not the case: there is a single vector space, $$V,$$ and only one zero element of $$V.$$
What we are trying to show is ultimately set-theoretic in nature: we want to show that if an element $$v\in\bigcap_{i=1}^{n}\text{ker}(T_{i}),$$ then $$v\in \text{ker}\left(\sum_{i=1}^{n}T_{i} \right).$$ Let's break down what all this means:
To say that a vector belongs to the kernel of a linear transformation means that the linear transformation sends that vector to zero. So, by assuming $$v\in\bigcap_{i=1}^{n}\text{ker}(T_{i})$$ we are saying that $$v$$ makes all of the linear transformations zero; i.e.
$$T_{1}(v)=0,~ T_{2}(v)=0,\ldots, T_{n}(v)=0$$
In each case above the zero is the zero element of $$V,$$ they are not different zeros. Now, to show that $$v\in \text{ker}\left(\sum_{i=1}^{n}T_{i} \right),$$ we must show that when we plug $$v$$ into the function/linear transformation $$\sum_{i=1}^{n}T_{i}$$ we still get zero. For this we compute:
$$\left( \sum_{i=1}^{n}T_{i}\right)(v)=\sum_{i=1}^{n}T_{i}(v)=T_{1}(v)+T_{2}(v)+\ldots+T_{n}(v)=0+0+\ldots+0=0$$
Hence, $$v\in\text{ker}\left(\sum_{i=1}^{n}T_{i} \right).$$ Since $$v\in\bigcap_{i=1}^{n}\text{ker}(T_{i})$$ was arbitrary, the proof is finished.
Let's take an example to help us along. Let our vector space be
$$V=\mathbb{R}^{3}=\left\{\begin{bmatrix}x\\ y\\ z \end{bmatrix}: x, \, y, \, z\in\mathbb{R} \right\}$$
and our linear transformations $$T_{1}$$ & $$T_{2}$$ be given by
$$T_{1}\left(\begin{bmatrix}x\\y\\z \end{bmatrix} \right)=\begin{bmatrix}0\\y\\0 \end{bmatrix}$$
and
$$T_{2}\left(\begin{bmatrix}x\\y\\z \end{bmatrix} \right)=\begin{bmatrix}x\\0\\0 \end{bmatrix}$$
The zero element in this example is $$\begin{bmatrix}0\\0\\0\end{bmatrix}$$
Notice that $$T_{1}\left(\begin{bmatrix}x\\y\\z \end{bmatrix} \right)=\begin{bmatrix}0\\0\\0\end{bmatrix}$$
if and only if $$y=0.$$ Hence, $$\text{ker}(T_{1})=xz$$ plane. Similarly, $$\text{ker}(T_{2})=yz$$ plane. The intersection of these two kernels is the entire $$z$$ axis; i.e.
$$\bigcap_{i=1}^{2}\text{ker}(T_{i})=\left\{\begin{bmatrix}0\\0\\z \end{bmatrix}: z\in\mathbb{R} \right\}$$
(Drawing a picture of the two planes to see that their intersection is the $$z$$ axis may be helpful)
Now, if we wish to demonstrate the general proof you're working on in this example, we take an element $$\begin{bmatrix}0\\0\\z\end{bmatrix}\in \bigcap_{i=1}^{2}\text{ker}(T_{i})$$ and compute using the definitions of $$T_{1}$$ & $$T_{2}$$
$$\left(T_{1}+T_{2}\right)\left(\begin{bmatrix}0\\0\\z\end{bmatrix} \right)=T_{1}\left(\begin{bmatrix}0\\0\\z\end{bmatrix} \right)+T_{2}\left(\begin{bmatrix}0\\0\\z\end{bmatrix} \right)=\begin{bmatrix}0\\0\\0 \end{bmatrix} + \begin{bmatrix}0\\0\\0 \end{bmatrix} = \begin{bmatrix}0\\0\\0 \end{bmatrix}
$$
Hence, $$\begin{bmatrix}0\\0\\z\end{bmatrix}\in\text{ker}\left(\sum_{i=1}^{2}T_{i} \right)$$ as well. Thus, for this specific example,
$$\bigcap_{i=1}^{2}\text{ker}(T_{i})\subseteq \text{ker}\left(\sum_{i=1}^{2}T_{i} \right),$$
as it should be from your general exercise.
This is a long post, but I hope I have understood and addressed your concern. Let me know if anything is unclear/not quite right.
Cristian1
- 3
- 0
thank you very much! :)
It is well known that a vector space always admits an algebraic (Hamel) basis. This is a theorem that follows from Zorn's lemma based on the Axiom of Choice (AC).
Now consider any specific instance of vector space. Since the AC axiom may or may not be included in the underlying set theory, might there be examples of vector spaces in which an Hamel basis actually doesn't exist ?
Similar threads
- Replies
- 1
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 3
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 23
- Views
- 1K
- Replies
- 7
- Views
- 699
- Replies
- 9
- Views
- 3K
- Replies
- 4
- Views
- 1K
- Replies
- 3
- Views
- 2K
Hot Threads
-
I Showing ##k[x_1,\ldots,x_n]/\mathfrak{a}## is finite dimensional
- Started by elias001
- Replies: 40
- Linear and Abstract Algebra
-
A Near-Rings with Noncommutative Addition and Two-Sided Distributivity
- Started by lpetrich
- Replies: 4
- Linear and Abstract Algebra
-
I How do we distinguish two different notations for cokernel and coimage?
- Started by elias001
- Replies: 41
- Linear and Abstract Algebra
-
I Localising a non integral domain at a prime
- Started by elias001
- Replies: 17
- Linear and Abstract Algebra
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math