ksio89
- 4
- 1
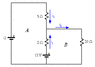
I'm trying to solve item "c" of this question about the electrical circuit depicted on the attached picture.
The question is in Brazilian Portuguese, this would be a rough and not 100% gramatically correct translation:
"In the circuit shown below on Pic. 1 (labeled "Electrical Circuit"), the three resistors have values R_1 = 2 Ω, R_2 = 20 Ω and R_3 = 5 Ω. The battery B has constant tension 12 V. The current i_1 is considered positive in the indicated direction. Between the instants t = 0 s and t = 100 s, the generator G provides a variable tension V = 0.5 t (V in volts and t in seconds).
a) Define the current value i_1 for t = 0 s
b) Define the instant t_0 in which the current i_1 is null.
c) Plot the curve which depicts the current i_1 in function of the time t, in the interval from 0 to 100 s. Use the axis from the following picture (labeled "Graph") and clearly indicate the scale of current, in ampère (A).
d) Define the value of the power P received or provided by the battery B in the instant t = 90 s."
I was able to solve items a, b and d using Kirchoff's Voltage Law and generating a linear system with two variables, i'_1 and i'_2, where i'_1 \pm i'_2 = i_1 and i'_1 is the current flowing around the left loop (loop I) and i'_2 is the current flowing around the right one (loop II). So:
a) 2 s;
b) t = 30 s (in this case, i'_1 = -i'_2;
c) ?
d)P = (I need to find the graph of i_1 vs. t so I can calculate the absolute value of the power).
I wasn't able able to answer item c, because it asks to plot the graph of i_1 Vs t. The issue is that i_1 is actually the algebric sum of i'_1 and i'_2, but I also have a third variable which is the tension V generated by the voltage source G, which is a function of time t. I don't have a third equation though, as Kirchoff's Voltage Law applied to the largest loop provides me an equation which is simply a linear combination of the equations associated with loops I and II.
According to the book answers section, the answer for item c) is a line of slope-intercept form f(t)= -\frac{t}{15}+2. Then, |P| would be 48 W. But how do you define i_1 as a function of V and, consequently, t?
The question is in Brazilian Portuguese, this would be a rough and not 100% gramatically correct translation:
"In the circuit shown below on Pic. 1 (labeled "Electrical Circuit"), the three resistors have values R_1 = 2 Ω, R_2 = 20 Ω and R_3 = 5 Ω. The battery B has constant tension 12 V. The current i_1 is considered positive in the indicated direction. Between the instants t = 0 s and t = 100 s, the generator G provides a variable tension V = 0.5 t (V in volts and t in seconds).
a) Define the current value i_1 for t = 0 s
b) Define the instant t_0 in which the current i_1 is null.
c) Plot the curve which depicts the current i_1 in function of the time t, in the interval from 0 to 100 s. Use the axis from the following picture (labeled "Graph") and clearly indicate the scale of current, in ampère (A).
d) Define the value of the power P received or provided by the battery B in the instant t = 90 s."
I was able to solve items a, b and d using Kirchoff's Voltage Law and generating a linear system with two variables, i'_1 and i'_2, where i'_1 \pm i'_2 = i_1 and i'_1 is the current flowing around the left loop (loop I) and i'_2 is the current flowing around the right one (loop II). So:
a) 2 s;
b) t = 30 s (in this case, i'_1 = -i'_2;
c) ?
d)P = (I need to find the graph of i_1 vs. t so I can calculate the absolute value of the power).
I wasn't able able to answer item c, because it asks to plot the graph of i_1 Vs t. The issue is that i_1 is actually the algebric sum of i'_1 and i'_2, but I also have a third variable which is the tension V generated by the voltage source G, which is a function of time t. I don't have a third equation though, as Kirchoff's Voltage Law applied to the largest loop provides me an equation which is simply a linear combination of the equations associated with loops I and II.
According to the book answers section, the answer for item c) is a line of slope-intercept form f(t)= -\frac{t}{15}+2. Then, |P| would be 48 W. But how do you define i_1 as a function of V and, consequently, t?
Attachments
Last edited: