Zinggy
- 12
- 0
Homework Statement
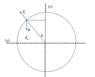
A small bead of mass m slides on a frictionless cylinder of radius R which lies with its cylindrical axis horizontal. At t = 0 , when the bead is at (R,0), vz = 0 and the bead has an initial angular momentum Lo < mR sqrt(Rg) about the axis of the cylinder where g is the acceleration due to gravity. The bead slides from (R,0) down the curved surface of the cylinder and eventually loses contact with that surface.
Find r(double dot) in Cylindrical Coordinates.
2. Homework Equations
Position Vector of r = ˆ iRcosφ + ˆ jRsinφ = ρˆR
The Attempt at a Solution
I know r(double dot) is the same as d2r/dt2 so;
r = ˆ iRcosφ + ˆ jRsinφ = ρˆR
r(dot) =- iRsinφ+jRcosφ -unless R changes with time, which I don't think it does.
then
r(double dot) = iR-cosφ - jRsinφ
I think I'm missing something. Do I need to include the angular momentum somewhere?