Kinetics friction question: derive acceleration of aircraft

[LauraMorrison]

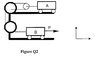
1. Hello there, I am a first year undergraduate mechanical engineering student, looking for help on a question. "Figure Q2 shoes a schematic diagram for an aircraft catapult system. The aircraft is represented by the mass A (Ma), and μ is the coefficient of friction between the aircraft and deck. Mass B (Mb) represents the mass of the catapult system. Show that the acceleration of the aircraft is given by:
\ddot{x}a = (-2P + μMag)/(Ma + 4Mb)
http://www.flickr.com/photos/90819422@N06/8247087046/in/photostream/




2. ƩF = ma



3. I first drew out the FBD of the two masses. I was unsure of the direction of the friction forces for each mass and if there even is a friction force for mass B? I was also unsure if the tension in the rope at mass B is equal to the force P? I have also attached the figure in this post. Please Help, my exam is next week!

 

[WillemBouwer]

I cannot see your figure but am able to see your FBD, the tension in a rope should be uniform throughout the length of a rope, so by drawing a FBD for only Mass B what is the tension in the rope? There is no mention of a friction coefficient at Mass B so assume there are none and only at mass A.
What is the forces acting on the aircraft(Mass A)? Draw a FBD for mass A alone...

 

[LauraMorrison]

I assume then that the tension in the rope at B is P, and the tension at A is 2P? However, doing this means that when I write F=ma for mass B, the sum of the forces in the x direction is zero since P and P cancel out? Surely this cannot be right?

 

[WillemBouwer]

Yes I agree, must have put that wrong, draw FBD's for both your masses. Let's start there and give the tension in your rope a value of T...
Draw this and let's move from there. Choose a positive direction for your axis.
Also from inspection what do you think the acceleration of A would be in terms of the acceleration of B?

 

[LauraMorrison]

Hi there, I have done the FBD for both masses and I have got to a certain point but I am stuck on mass B as the acceleration keeps adding to zero.. making it hard to do anything with the equation! I have attached my working to this message. Thanks for your help, I really appreciate it.

 

[WillemBouwer]

So the equations you have is:
-T_a + μM_ag = m_a*x_a for A
note x_a is acceleration of a...
-T_b + P = m_b*x_b
note x_b is acceleration of b...
you stated that T_a = 2T_b so substitute that into equation 1.

You state that Tb = -P? This should not be assumed, because that will result in no acceleration indeed...
Try defining equation 2 in terms of T_b, and substitute that into equation 1 in the place of T_b, see where I'm going with this? you now eliminated T_b to get P into your equation... We will work from there.

 

[LauraMorrison]

YES! I got it.
So the acceleration of A is -0.5 * the acceleration of B? and then substituting equation 2 into equation one along with the acceleration of A gives the correct answer. Thanks so much!

 

[WillemBouwer]

YES! Big pleasure glad I could help...