Kirchoff's Rule(How do I find equivalent resistance?)

In summary: Actually, if you note that there are "missing" resistors on the diagonals you might see that direct simplification is quite possible.
  • #1
jawhnay
37
0

Homework Statement


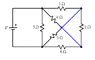
Please take a look at the attachment to see the circuit. My question is how do I find the equivalent resistance of this circuit? I have done the other two parts but this part has got me stumped. I also drew my currents on the picture.


Homework Equations





The Attempt at a Solution


I attempted to categorize which resistors were in parallel and in series to each other but that just got me really confused... If anyone can walk me through this problem it would be greatly appreciated.

Here are my loop equations:

-9I1+3I2+9I3+8I4 = -12
-3I3 = -12
-6I1-4I2+6I3+6I4 = -12
-I1+I2+I3-5I4 = -12

I1 = 7.324841
I2 = 0.878981
I3 = 4
I4 = 1.910828

current across the 5 ohm resistor = 1.911 amps
Vab = -8.484 volts
 

Attachments

  • kirchoff.png
    kirchoff.png
    7.6 KB · Views: 548
Last edited:
Physics news on Phys.org
  • #2
Do you know how to write loop equations? You need to show some effort on your own so we know where you are stumped. Just giving the answer is against forum rules.

EDIT: "walking you through it" is equivalent to giving the answer. We're more into hints.
 
  • #3
yes, I know how to write loop equations. However, I thought the equivalent resistance was just adding up the resistances so I didn't think I would need to show my loop equations. I have edited my first post with the loop equations and edited picture.
 
Last edited:
  • #4
Since you have the current being drawn out of the 12V supply, you have the equivalent resistance, yes?

The problem is that "adding up the resistances" just doesn't work unless everything is simple series/parallel combinations and you've already figured out that that is not the case with this circuit else you would have been able to do it.
 
  • #5
oh my gosh, I cannot believe I didn't see it. Thank you for the help!
 
Last edited:
  • #6
phinds said:
Since you have the current being drawn out of the 12V supply, you have the equivalent resistance, yes?

The problem is that "adding up the resistances" just doesn't work unless everything is simple series/parallel combinations and you've already figured out that that is not the case with this circuit else you would have been able to do it.

Actually, if you note that there are "missing" resistors on the diagonals you might see that direct simplification is quite possible. Easy in fact :smile:

attachment.php?attachmentid=58108&stc=1&d=1366631112.gif
 

Attachments

  • Fig1.gif
    Fig1.gif
    2.1 KB · Views: 686

FAQ: Kirchoff's Rule(How do I find equivalent resistance?)

1. What is Kirchoff's Rule and why is it important?

Kirchoff's Rule, also known as Kirchoff's Laws, are fundamental principles used to analyze and solve complex electrical circuits. They help ensure that the conservation of charge and energy are maintained within a circuit, and are essential for designing and troubleshooting electrical systems.

2. How do I apply Kirchoff's Rule to find equivalent resistance?

To find equivalent resistance using Kirchoff's Rule, you must first identify all the resistors in the circuit and label them with their respective values. Then, use Kirchoff's First Law, also known as the Law of Conservation of Charge, to write equations for the currents flowing into and out of each node in the circuit. Finally, use Kirchoff's Second Law, also known as the Law of Conservation of Energy, to write equations for the voltage drops across each resistor. These equations can then be solved simultaneously to find the equivalent resistance of the circuit.

3. Can Kirchoff's Rule be applied to any type of circuit?

Yes, Kirchoff's Rule can be applied to any type of circuit, whether it is a series, parallel, or a combination of both. It is a universal principle that applies to all electrical circuits, regardless of their complexity.

4. What are the limitations of Kirchoff's Rule?

Kirchoff's Rule assumes ideal conditions, such as no resistance in wires, no temperature changes, and no electromagnetic interference. In reality, these ideal conditions are not always met, which can lead to slightly different results than what is calculated using Kirchoff's Rule. Additionally, Kirchoff's Rule does not take into account the effects of inductance and capacitance, which may be significant in some circuits.

5. Are there any tips for using Kirchoff's Rule effectively?

One helpful tip is to label all the nodes and branches in the circuit to keep track of which equations correspond to which parts of the circuit. It is also important to double-check all your calculations and equations to ensure accuracy. Additionally, breaking down a complex circuit into smaller parts and applying Kirchoff's Rule to each part separately can make the overall analysis more manageable.

Similar threads

Find the equivalent resistance of this circuit
Replies
31
Views
2K
How can I calculate the equivalent resistance of this circuit?
Replies
9
Views
2K
Calculating current with and without internal resistance
Replies
6
Views
2K
What's Wrong with My Thevenin Equivalent Short-Circuit Current Calculation?
Replies
1
Views
954
How to solve this chain with Kirchhoff's laws?
Replies
18
Views
2K
Find the equivalent resistance (Req) of the simple circuit.
Replies
4
Views
3K
How Do You Solve Complex Kirchhoff's Law Problems?
Replies
5
Views
1K
Kirchoff's Laws Problem Current
Replies
11
Views
2K
What is the current through each resistor in this circuit?
Replies
4
Views
3K
How Do You Solve Mesh Analysis with Multiple Loops and Controlled Sources?
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top