Ladder Angular Momentum Problem

[Karol]

Homework Statement

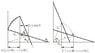
A ladder is leaning against a smooth wall and a smooth floor (no friction). it's starting to slide
down. The initial angle between the ladder and the floor is \theta₀, according to the drawing. The mass is m and length 2b.
It is clear that the distance from the center of mass to the corner is also b, and that the center of mass makes a circle when it moves.
At what angle does the ladder detaches.
I have a true solution and it is: sin\theta_c=(2/3)sin\theta_0, but I want to test another.
I also know the angular velocity of the ladder is the same as that of the center of mass around the corner and equals to:
\omega=\sqrt{3g/(2b)(\sin\theta_0-\sin\theta}
and the angular acceleration is:
\alpha=\dot{\omega}=-(3g/4b)\cos\theta

Homework Equations

Centrifugal force: F_c=m\omega^2R

The Attempt at a Solution

If I dismantle the gravitational force mg into 2 components: one directed towards the corner and the other tangent to the circle equal the center of mass makes, according to the drawing, and I try to equal the component that is directed towards the corner with the centrifugal force:
mg\cdot\sin\theta_c=m\frac {3g} {\sin\theta_0-\sin\theta_c}b
which gives a meaningless result.
Why isn't that principle good for this situation? it is the method for solving the problem of a point mass sliding down on a frictionless dome.

 

[kuruman]

I also know the angular velocity of the ladder is the same as that of the center of mass around the corner and equals to:
\omega=\sqrt{3g/(2b)(\sin\theta_0-\sin\theta}

How do you know this? What equation did you use to derive this result?

 

[Karol]

I took this answer from the book the problem was in.
The initial energy of the altitude the final energy: the one of the altitude plus the kinetic energy of the center of mass plus the energy due to rotation around the center of mass:
mgb{\sin\theta_0}=mgb{\sin\theta}+\frac{1}{2}m{V_c}^2+\frac{1}{2}I_c\omega^2=<br /> mgb{\sin\theta}+\frac{2}{3}mb^2\omega^2
Which yields:
\omega=\sqrt{3g/(2b)(\sin\theta_0-\sin\theta)}

 

[kuruman]

Is the angular speed ω of the CM about the corner the same as the angular speed of the ladder about the CM? Why is that?

 

[Karol]

Yes. that part I proved myself.
I dismantle (I'm not shure I'm usung the correct word, please correct me) the combined movement into two separate ones: translation and rotation, according to the drawing.
I assume the angle \theta is the same for the two rotations, and measure the horizontal distance A the m.c. makes and the edge of the stick, of course in the opposite direction.
We see, in the drawing, that they are the same:
b(\cos\theta_1-\cos\theta_2)

 

[hikaru1221]

Firstly, I can't see how you got the angular acceleration. Typo, maybe?
Secondly, I confirm that the angular speeds are fortunately the same So that's not the problem.
Thirdly, I believe the last equation you yielded is for when the ladder detaches, correct? If so, then you missed one force: the normal force by the ground

 

[Karol]

I'm somehow new to forums, I don't know what the slang word "typo" means, please explain.
The angular acceleration is from the book. simply the derivative of the angular velocity.
No, the last equation
<br /> b(\cos\theta_1-\cos\theta_2)<br />
is not for the point of detachement, it is a general point, it is just a trigonometric calculation of distances.
I know there are normal forces from the walls, probably yielding together the normal as if the ladder was a point mass on a sphere. that's what i ask, why can't I solve this problem as if it were a point mass and a normal force acting upon it. as I showed in the beginning, this approach does not yield result.
The approach the book took is combining the radial and the tangent accelaration, and demanding that it be vertical. It's clear, since after it detaches it falls down, with initial velocity, of course.

 

[hikaru1221]

Typo = mistyped word (it's standard English btw)
1/ The angular acceleration should be different. Calculate it again.
2/ Huh? b(\cos\theta_1-\cos\theta_2) is not even an equation.
I really don't get what you are saying. Can you explain this equation of yours?
<br /> mg\cdot\sin\theta_c=m\frac {3g} {\sin\theta_0-\sin\theta_c}b<br />

 

[Karol]

1) I gave the angular acceleration:
\alpha=\dot{\omega}=-(3g/4b)\cos\theta
Just in case you'd need it. I copied from the book, but I would check again if necessary.

2) b(\cos\theta_1-\cos\theta_2) is not a formula. It is the horizontal distance the m.c. and the edge of the stick make while moving from initial state in \theta_1 to \theta_2. I used it only to prove that the m.c. and the ladder both move with the same angular velocity \omega. You don't need it.

3) The formula:
mg\cdot\sin\theta_c=m\frac {3g} {\sin\theta_0-\sin\theta_c}b
Is based on: \Sigma\mbox{F}=ma, where a is the centrifugal acceleration \omega^2R.
mg\cdot\sin\theta_c is the component of the gravitational force mg, that is (the component) directed during the whole circular motion to the corner, the center of the circle the m.c. makes. The subscript c below the \theta denotes it is at the detachment point.
See drawing.

 

[hikaru1221]

1/ If you differentiate your \omega, you won't get that acceleration.
2/ Oh, sorry, I meant the last equation in the #1 post, and you thought it was the last expression of yours which is in post #7. Just misunderstanding.
3/ Again, you missed the normal force from the ground, or more exactly, the component of that normal force perpendicular to the ladder. \Sigma \vec{F} must include it. Have a look at this:
http://en.wikipedia.org/wiki/Center_of_mass#Derivation_of_center_of_mass
The motion of CM is like that of a point mass which experiences ALL the external forces acting on the ladder (i.e. mg & normal forces), not just the forces acting at CM on the ladder (i.e. mg).

By the way, I think the last equation of yours in post #1 is a bit incorrect. It should be: <br /> mg\cdot\sin\theta_c=m\frac {3g} {\sin\theta_0-\sin\theta_c}<br />. No "b" included.

 

[Karol]

You are right, there are 2 normal forces from the wall & floor. But I need 2 <br /> \Sigma\mbox{F}=ma equations for that, one for each axis, and the MC movement is complex.
Any how, I'm looking for an elegant solution, and this is not.
I understand the normal forces are also forcing a moment on the rod. They are not only acting on the MC. So my method was wrong, I can't solve it like it was a point mass.
What is your suggestion, other than that of the book, which I described earlier.

 

[hikaru1221]

I understand the normal forces are also forcing a moment on the rod. They are not only acting on the MC. So my method was wrong, I can't solve it like it was a point mass.

It seems that you haven't got my point. I didn't say anything about moments. The problem is, when you consider the motion of CM, you must treat it as a point mass which experiences ALL the forces acting on the whole ladder. So the normal force must be included, which results in:
mg\cdot\sin\theta_c-Nsin\theta_c=m\frac {3g} {\sin\theta_0-\sin\theta_c}
where N is the normal force by the ground.

I believe although there might be other solutions, the solution of the book is the shortest. The condition of the detachment is that the normal force by the wall = 0, and when it comes to force, force analysis is inevitable. This condition leads directly to the solution of the book, so there is no other way.

 

[Karol]

By the way, I think the last equation of yours in post #1 is a bit incorrect. It should be: mg\cdot\sin\theta_c=m\frac {3g} {\sin\theta_0-\sin\theta_c}. No "b" included.

I think "b" should be included, but in the denominator:
mg\cdot\sin\theta_c=m\frac {3g} {2b(\sin\theta_0-\sin\theta_c)}

The condition of the detachment is that the normal force by the wall = 0

It is logical that when it detaches it moves away from the wall. But why are you so sure it is still accelerating angularly by the normal from the floor?
In short, maybe at detachment point all normals zero.

 

[hikaru1221]

I think "b" should be included, but in the denominator:
mg\cdot\sin\theta_c=m\frac {3g} {2b(\sin\theta_0-\sin\theta_c)}

No. Check the dimension. The left side has the dimension of force, while the right side has the dimension of force over length.

EDIT: Btw, I think the correct one should be: (mg-N)\sin\theta_c=m\frac {3g(\sin\theta_0-\sin\theta_c)}{2}. I misread your angular velocity. It is \omega = \sqrt{\frac{3g}{2b}(sin\theta_o-sin\theta) so the term (sin\theta_o-sin\theta) should be in the numerator.

It is logical that when it detaches it moves away from the wall. But why are you so sure it is still accelerating angularly by the normal from the floor?
In short, maybe at detachment point all normals zero.

At the time of detachment, normal force by the wall = 0, agree?
Now that "maybe" of yours should be checked. The normal force by the ground is either zero or non-zero, so adding it to the equation won't make any difference: if it's zero, it will disappear, if it's not, it remains in the equation. But if you don't include it in the equation, it would be fine if it's zero, but it's another story if it's not. So it's safe when we include the normal force, and it's not safe when we don't.

I shall now prove that the normal force by the ground is not zero at the time of detachment. We have at the time of detachment: m\vec{g}+\vec{N}=m\vec{a}_{centripetal}+m\vec{a}_{tangent}

Thus:

ma_{tangent}=m\alpha b=(mg-N)cos\theta_c

Moreover:

\alpha=\dot{\omega}=\frac{d}{dt}\sqrt{\frac{3g(sin\theta_o-sin\theta)}{2b}}=\sqrt{\frac{3g}{2b}}\times\frac{-cos\theta}{2\sqrt{sin\theta_o-sin\theta}}\times\frac{d\theta}{dt}

Notice that: \omega = - d\theta/dt, we get:

\alpha=3gcos\theta/ (4b)

Therefore, at the time of detachment:

3mgcos\theta_c/4=(mg-N)cos\theta_c

So: N=mg/4\neq 0

 

[Karol]

1)

We have at the time of detachment: m\vec{g}+\vec{N}=m\vec{a}_{centripetal}+m\vec{a}_{tangent}

Thus:

ma_{tangent}=m\alpha b=(mg-N)cos\theta_c

Why "Thus"? equation:ma_{tangent}=m\alpha b=(mg-N)cos\theta_c
Is a new, stand alone one. I understand it is: \Sigma\mbox{F}=ma in the tangent direction. It is not derived directly from:m\vec{g}+\vec{N}=m\vec{a}_{centripetal}+m\vec{a}_{tangent} since where is m\vec{a}_{centripetal}?
2) Why the minus sign in \omega = - d\theta/dt?
What does a minus angular velocity mean? is it a vector? does it denote direction of angular motion? if so, then the motion of which element: MC moves clockwise while the rod rotates at the same \omega in the opposite direction.

 

[hikaru1221]

1/ Oh, by "tangent" I mean "tangent to the orbit". In this case, "centripetal" is towards the center of the circular orbit, and "tangent" is perpendicular to that direction of "centripetal".
So first, the Newton 2nd law says \Sigma\vec{F}=m\vec{a}, NOT \Sigma F=ma. Second, I derived that equation directly from the Newton 2nd law equation. Project all vectors in the Newton 2nd law equation onto the "tangent" direction and you will get that equation.

2/ If it were a vector, there should be an arrow sign above it like this \vec{\omega} (many Western textbooks print vectors in bold instead of adding the arrow sign, but I don't know how to make them bold in Latex, so I use the arrow sign instead).
And yes, it says something about the direction of angular motion. It only makes sense when it denotes the angular speed of CM, because we're considering the motion of CM.
Then why the minus sign? Look back at post #3 where you derived \omega. There are actually 2 solutions: \omega=\sqrt{3g/(2b)(\sin\theta_0-\sin\theta)} and \omega=-\sqrt{3g/(2b)(\sin\theta_0-\sin\theta)}. You omitted the latter (x^2=4 yields x=2 or x=-2, correct?). So when you choose the positive solution, that means \omega you choose is angular speed (or magnitude of velocity). It doesn't tell us anything about the direction of the circular motion of CM. But fortunately, we know that \theta decreases with time, so d\theta/dt&lt;0. Besides, we also know that |\omega|=|d\theta/dt|. Therefore: \omega=-d\theta/dt.

 

[Karol]

Thank you very much for your patience, indeed I am a bothersome patient...
I reserve myself the right to ask again, when in need.
Thanks.