- #1
hanyas
- 7
- 0
I'm trying to write down the equations of motion for a tetherball moving in 3D around a pole while the string is getting shorter.I've started with lagrange equations:
[itex]
x(t)=l(t) \sin (\theta) \cos (\phi)\\
y(t)=l(t) \sin (\theta) \sin (\phi)\\
z(t)=h(t)+l(t) \cos(\theta)\\ \\
T = \frac{1}{2}m(\dot x^2 +\dot y^2+\dot z^2)\\
U=m g l(t)(1-\cos(\theta)) + mg(S-(h(t)+l(t)))
[/itex]
where [itex]l(t)[/itex] is the length of the string. Here only I am assuming the radius of the pole is really small compared to [itex]l[/itex]. The polar angle is [itex]\theta(t)[/itex]. [itex]h(t)[/itex] is the change in height due to the string wrapping on the pole. [itex]S[/itex] is the length of string when unwrapped.
The change in length along is given by:
[itex]
\dot l(t) = -\frac{r\dot\phi}{ \sin(\theta)}
[/itex]
where [itex]r[/itex] is the radius of the pole. And the sliding pivot point is given by:
[itex]
\dot h(t) = \frac{r\dot\phi}{ \tan(\theta)}
[/itex]
After plugging those in [itex]T[/itex] I apply the Lagrange derivative to [itex]L = T-U[/itex] and solve for [itex]\ddot \theta[/itex] and [itex]\ddot \phi[/itex]
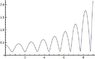
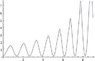
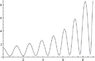
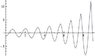
Now when I simulate the results I get a linear velocity that is some how increasing which is not supposed to happen for a tetherball because no new energy has been introduced to the system and the angular momentum is not conserved.
I would appreciate some feedback
[itex]
x(t)=l(t) \sin (\theta) \cos (\phi)\\
y(t)=l(t) \sin (\theta) \sin (\phi)\\
z(t)=h(t)+l(t) \cos(\theta)\\ \\
T = \frac{1}{2}m(\dot x^2 +\dot y^2+\dot z^2)\\
U=m g l(t)(1-\cos(\theta)) + mg(S-(h(t)+l(t)))
[/itex]
where [itex]l(t)[/itex] is the length of the string. Here only I am assuming the radius of the pole is really small compared to [itex]l[/itex]. The polar angle is [itex]\theta(t)[/itex]. [itex]h(t)[/itex] is the change in height due to the string wrapping on the pole. [itex]S[/itex] is the length of string when unwrapped.
The change in length along is given by:
[itex]
\dot l(t) = -\frac{r\dot\phi}{ \sin(\theta)}
[/itex]
where [itex]r[/itex] is the radius of the pole. And the sliding pivot point is given by:
[itex]
\dot h(t) = \frac{r\dot\phi}{ \tan(\theta)}
[/itex]
After plugging those in [itex]T[/itex] I apply the Lagrange derivative to [itex]L = T-U[/itex] and solve for [itex]\ddot \theta[/itex] and [itex]\ddot \phi[/itex]
Now when I simulate the results I get a linear velocity that is some how increasing which is not supposed to happen for a tetherball because no new energy has been introduced to the system and the angular momentum is not conserved.
I would appreciate some feedback
Last edited:


 )
)