Klas
- 5
- 0
Homework Statement
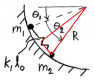
Two masses are connected by a weightless spring in a friction-less semicircular well (Picture included). Derive the equations of motion with help of lagrange
Homework Equations
L = T - U = kinetic energy - potential energy
The Attempt at a Solution
##L = \frac{1}{2}m_1(\dot{x_1}^2 + \dot{y_1}^2) + \frac{1}{2}m_2(\dot{x_2}^2 + \dot{y_2}^2) - (m_1gx_1 + m_2gx_2 + \frac{1}{2}k(\sqrt{x^2-y^2} -l_0)^2)##
Where:
##x_1 = R\cos\theta_1, \;\;x_2 = R\cos(\theta_1+\theta_2) \\y_1 = R\sin\theta_1, \;\;y_2 = R\sin(\theta_1+\theta_2)##
##x=x_2-x_1##
##y=y_2-y_1##
I think I'm going to be able to get the equation of motion from here if only L is right...
And if it's correct it feels like the EOM will be a pain in the ass from here but it feels like I'm missing something rather essential here?
I'll be thankful for any help
Last edited: