StevenJacobs990
- 16
- 0
The equation for large-angle pendulum can be infinitely long. What is the pattern with the latter numbers in "..."?
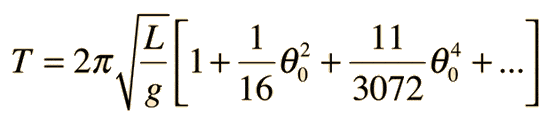
The discussion centers on the equation for large-angle pendulums, specifically the complexities of its infinite series representation. Participants highlight the necessity of elliptic integrals for accurate calculations and speculate on the potential use of Taylor expansions in deriving the series. A pendulum calculator, capable of calculating periods up to theta 14 using the arithmetic mean, is also shared by a user, providing a practical tool for further exploration of the topic.
PREREQUISITESStudents of physics, mathematicians, and engineers interested in pendulum mechanics and those developing tools for calculating pendulum dynamics.
Yeah, but what's the pattern that comes after 11/3072 (theta)^4?sophiecentaur said:Does this link help?
AS I said before, your attachment is not readable.StevenJacobs990 said:Yeah, but what's the pattern that comes after 11/3072 (theta)^4?
. . . .or something else. There are (my Mathematician friends tell me) many equations that can only be solved using a series - Taylor or not so well known ones.rumborak said:Honestly, I wouldn't be surprised if this a Taylor expansion of some sort.