Large n-pt functions renormalized by small n-pt functions?

[geoduck]

Suppose you have a λφ⁴ theory. Books only seem to calculate counter-terms for 2-pt and 4-pt functions.

But what about 3 particles scattering into 3 particles? Do the counter-terms determined by renormalizing the 2-pt and 4-pt functions cancel divergences in 3x3 scattering?

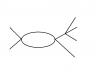
For example, take the graph below:

Is it obvious that the counter-terms from 2x2 and scattering, along with counter-terms from the 2-pt function, can cancel this graph?

 

[The_Duck]

In a renormalizable theory, the counterterms that you introduce to cancel the divergences in a few basic n-point functions suffice to cancel the divergences in all n-point functions.

I think the intuitive reason for this is: the more propagators you add to a loop, the more convergent the loop integral becomes. So large n-point functions generally aren't divergent unless they contain a divergent subdiagram with a small loop. But the divergences in those small loops will be canceled by the counterterms that you introduced to make the small n-point functions finite.

For example look at the attached diagram that contributes to the 6-point function in $\phi^4$ theory. The loop has three propagators, so the loop integral goes like $\int d^4 p / p^6$, which is convergent. The second attached image shows a divergent diagram contributing to the 6-point function. However the divergent loop looks just like one of the divergent contributions to the 4-point function, so it should be canceled by the same counterterm that cancels the divergence in the 4-point function.

In your diagram, I think the only divergent loop is the topmost loop. This divergence should be canceled by the same counterterm that cancels the divergences in the 4-point function.

I think there are nontrivial cases where there are "interlocking" divergent loops and it's not totally obvious that these ideas go through without doing some careful work, but this is the general picture.

Peskin & Schroeder sections 10.4 and 10.5 discuss these issues.