Laws of Motion with Static Equilibrium

AI Thread Summary
The discussion focuses on solving a static equilibrium problem involving two weights and tensions in ropes. The user attempts to find the angles and tensions using equations related to forces and trigonometry but struggles to obtain the correct answers. They clarify that the vertical component of tension T_1 corresponds to the weight w_1, leading to a calculation of T_1 as 17.447 N. The conversation also touches on the role of pulleys in changing the direction of tension without affecting its magnitude. The user seeks confirmation on their approach and calculations regarding the tensions in the ropes.
Keithkent09
Messages
33
Reaction score
0

Homework Statement


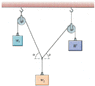
Find θ and W in the figure below where w1 = 16.0 N, w2 = 25.0 N, and α = 66.5°, assuming that the arrangement is at rest.

Homework Equations


T_1=25/sin(alpha)
F_x=-T_1cos(alpha)+T_2cos(theta)
F_y=T_1sin(alpha)+T_2sin(theta)-2

The Attempt at a Solution


I tried to use the above equations to solve for the three unknowns. First I found the tension of the string on the left, then plugged that into the second two equations to find the remaining values and I could not get the correct answers.
 

Attachments

  • weights.gif
    weights.gif
    12.6 KB · Views: 747
Physics news on Phys.org
Keithkent09 said:
T_1=25/sin(alpha)

Why is this true? What are tensions T1 and T2 in each rope?
 
Sorry I meant that it is 16/sin(alpha).
This is because the vertical component of T_1 is 16 because of w_1. So using trig T_1=17.447. I am doing this the correct way and just making some kind of simple mistake?
 
A pulley changes the direction of the tension without changing its magnitude. What is the tension in the piece of the leftmost rope that is hanging straight down?
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Rope between inclines with maximum length of hanging middle portion
Replies
46
Views
2K
Static equilibrium: setting up the equation
Replies
11
Views
3K
What is the Direction of Normal Force in Static Equilibrium on a Ramp?
Replies
5
Views
1K
Spring static equilibrium Problem
2
Replies
57
Views
6K
Find angle for the ring to be in equilibrium
Replies
2
Views
2K
Magnetic Field required to hold a loop in static equilibrium
Replies
5
Views
5K
How Does the Angle of Inclination Affect Motion in Rigid Body Dynamics?
Replies
6
Views
2K
Finding Total Charge from E-field
Replies
9
Views
3K
How Does Static Friction Maintain Equilibrium in a System of Balls?
Replies
16
Views
4K
Statics Problem, two disks in equilibrium
Replies
9
Views
5K

Hot Threads

Recent Insights

Back
Top