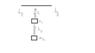
- #1
- 2,168
- 193
Homework Statement
a) If the distances ##s_1## and ##s_2## are the amounts the springs are streched while in static equilibirum, Write down the static equilibirum equations.
b) When the system is distrubed from its equilibirum state, both mases move vertically. Let ##y_1(t)## and ##y_2(t)## represent the displacement of masses from their equilibrium at time t. Write down the Newtons second law for each mass in terms of 2nd order DE.
c) For ##y_1(0)=y_2(0)=\dot y_1(0)= 0, \dot y_2(0) = 10## find the solution.
Homework Equations
The Attempt at a Solution
[/B]
Since the motion is always in one direction, I ll not use vector notation here.
Part(a) : Since its equi state the net force on bodies will be zero. Hence;
##0 = m_1g+k_2s_2-k_1s_1##
##0 = m_2g_2-k_2s_2##
For part (b)
The net force will be not zero this time. And I thought we can write
##m_1\ddot y(t)=m_1g+k_2y_2(t)-k_1y_1(t)##
##m_1\ddot y(t)=m_1g-k_2y_2(t)##
Are these equation true ? Cause later I need to solve these But I amhow also stuck how can I find the ##y_1(t)##