- #1
dstretan
- 3
- 0
This is a self-study homework problem. I am trying to verify the "falling column physics" associated with leaning forward with our center of mass in front of our feet.
Describe the free body diagram for a column (tree, pencil, person) leaning from vertical. Assume there are no forces at the ground inhibiting/resisting the forward fall. Also assume there is no force of air on the column as it moves forward.
- Newton's first three laws.
See the attached diagrams.
Vertical Column Preface:
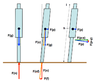
- The force of gravity acts downward on the column. This is depicted as F(g) acting on the column's center of mass (COM).
- A normal force F(n) opposes F(g).
Leaning Column:
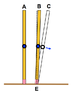
- The force of gravity acts downward on the column. This is depicted as F(g) acting on the column's center of mass (COM).
- This force F(g) has two components: F(c) acting down the column and F(p) acting perpendicular to the column as in a moment arm.
- Since the contact point with the ground is stationary, a normal force F(n) and a frictional force F(f) make up a force F(nf) equal and opposite to F(c).
- F(p) remains and acts on the COM which results in COM acceleration.
- F(p) has a F(p-x) and F(p-y) component, with movement x>y relative to f(h/l). Meaning the higher the center of mass the more x movement forward for y height decrease.
- The forces change as the position of the column moves forward relative to the contact point with the ground.
This might seem like a rather trivial physics problem but there are a lot of people who suggest that gravity cannot move a column/person forward. That is not my experience in terms of walking/running, and it would seem this simple diagram confirms the "feeling" of being moved forward by a series of micro-falls and micro-catches. The COM loses a small height with each fall, which it regains with each step.
- Moving downhill would mean it does not need to regain height; and probably not lean as much.
- Moving uphill would mean it would need to regain and add height; and possibly lean more.
- The person accelerates when falling - and decelerates otherwise (when in the air if we consider air resistance; and upon landing if we consider landing position and tension). The average velocity across the running gait cycle determines the runner's pace.
This answer might also explain how this "robot" is possible:
- http://www.wired.co.uk/news/archive/2011-10/26/bluebiped-robolegs
Similar examples might be a person walking on stilts or a unicyclist.
Your input would be greatly appreciated.
Thanks,
David.
Homework Statement
Describe the free body diagram for a column (tree, pencil, person) leaning from vertical. Assume there are no forces at the ground inhibiting/resisting the forward fall. Also assume there is no force of air on the column as it moves forward.
Homework Equations
- Newton's first three laws.
The Attempt at a Solution
See the attached diagrams.
Vertical Column Preface:
- The force of gravity acts downward on the column. This is depicted as F(g) acting on the column's center of mass (COM).
- A normal force F(n) opposes F(g).
Leaning Column:
- The force of gravity acts downward on the column. This is depicted as F(g) acting on the column's center of mass (COM).
- This force F(g) has two components: F(c) acting down the column and F(p) acting perpendicular to the column as in a moment arm.
- Since the contact point with the ground is stationary, a normal force F(n) and a frictional force F(f) make up a force F(nf) equal and opposite to F(c).
- F(p) remains and acts on the COM which results in COM acceleration.
- F(p) has a F(p-x) and F(p-y) component, with movement x>y relative to f(h/l). Meaning the higher the center of mass the more x movement forward for y height decrease.
- The forces change as the position of the column moves forward relative to the contact point with the ground.
This might seem like a rather trivial physics problem but there are a lot of people who suggest that gravity cannot move a column/person forward. That is not my experience in terms of walking/running, and it would seem this simple diagram confirms the "feeling" of being moved forward by a series of micro-falls and micro-catches. The COM loses a small height with each fall, which it regains with each step.
- Moving downhill would mean it does not need to regain height; and probably not lean as much.
- Moving uphill would mean it would need to regain and add height; and possibly lean more.
- The person accelerates when falling - and decelerates otherwise (when in the air if we consider air resistance; and upon landing if we consider landing position and tension). The average velocity across the running gait cycle determines the runner's pace.
This answer might also explain how this "robot" is possible:
- http://www.wired.co.uk/news/archive/2011-10/26/bluebiped-robolegs
Similar examples might be a person walking on stilts or a unicyclist.
Your input would be greatly appreciated.
Thanks,
David.