Lenz's Law Q: Clockwise or Counterclockwise?

[lenzlawquestion]

Homework Statement

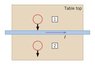
A long, straight wire lies on a table and carries a current I. As the drawing shows, a small circular loop of wire is pushed across the top of the table from position 1 to position 2. Determine the direction of the induced current, clockwise or counterclockwise, as the loop moves past position 1 and position 2.

Homework Equations

No equations, but the right hand grip rule is relevant.

The Attempt at a Solution

So I got the first part of the question right. I know that because the wire's current is going right, the right hand grip rule suggests that the magnetic field is pointing out of the screen/page. At position A, the table top has no field and the wire will want to resist the flux change. Therefore, a field will point downwards, opposite the direction of that of the wire, leading to a clockwise current at A.

However, B also has a clockwise current. My reasoning was that if the looped wire is within the field generated by the wire, its magnetic field would also be out of the screen/page, and therefore if it is pushed back to the flux-less table top, the flux would decrease. To oppose this, I thought that the secondary magnetic force would be out of the page, and the loop at B would be counterclockwise. So why is it actually clockwise?

 

[Hesch]

To oppose this, I thought that the secondary magnetic force would be out of the page, and the loop at B would be counterclockwise. So why is it actually clockwise?

In the first situation (1) the loop closes up the wire: the flux through the loop increases.
In the second situation the loop moves away from the wire ( the flux in the loop decreases ) but at the same time, the flux from the wire has changed direction:

http://onlinephys.com/magnet6.gif

 

[lenzlawquestion]

How do you know that the flux from the wire has changed direction? What causes it to be different from that in position A?

 

[Hesch]

How do you know that the flux from the wire has changed direction? What causes it to be different from that in position A?

Draw a line on the paper in the figure in #2, crossing the center/wire. This line is the surface of the table. Following this line in one direction, the flux will change sign when you cross the wire/center.

It's like crossing a road: Crossing the middle of the road, the traffic will come from the other side.