- #1
chetzread
- 801
- 1
Homework Statement
i'm not sure what is line integral...
Homework Equations
The Attempt at a Solution
Does it mean total length of line under the curve?
If f(x,y,z) = 1, then the line integral of this function over the curve C will give the arc length between a and b. If f(x,y,z) is some other function, this won't be the case.chetzread said:Homework Statement
i'm not sure what is line integral...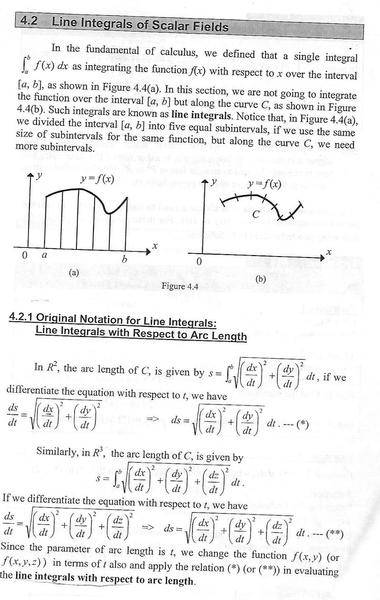
Homework Equations
The Attempt at a Solution
Does it mean total length of line under the curve?
If f(x,y,z) is some other function , what would it be?SteamKing said:If f(x,y,z) = 1, then the line integral of this function over the curve C will give the arc length between a and b. If f(x,y,z) is some other function, this won't be the case.
Who knows?chetzread said:If f(x,y,z) is some other function , what would it be?
Then, how about s( in the first photo in first post) only ? It represents the total length of curve?LCKurtz said:If for example ##f(x,y,z)## is the density per unit length of a wire, say in kg/m, then the integral ##\int_C f(x,y,z)~ds## would represent the total kg for the wire.
c
No. s is the cumulative distance along the curve, starting from a specified location.chetzread said:Then, how about s( in the first photo in first post) only ? It represents the total length of curve?
A line integral is a type of integral used to calculate the total length of a curve. It involves integrating a function over a given path, which can be a curve or a line segment.
To solve for the total length of a curve using a line integral, you need to divide the curve into small segments and then integrate the function over each segment. Finally, you add up all the individual lengths to get the total length of the curve.
The formula for calculating a line integral is: ∫ab √(1 + (dy/dx)2) dx, where a and b are the starting and ending points of the curve.
No, line integrals can also be used to calculate other quantities such as work, mass, and electric flux. The formula may vary depending on the quantity being calculated, but the basic concept remains the same.
Yes, line integrals cannot be used for curves that are not smooth, meaning that they have sharp corners or discontinuities. In such cases, other methods such as arc length parameterization or piecewise integration may be used to calculate the length of the curve.