Ty Ellison
- 3
- 0
Homework Statement
[/B]
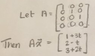
Suppose the solution set of some system Ax = b , Where A is a 4x3 matrix, is
*Bold characters are vectors*
x_1= 1 + 3t
x_2 = 2 - t
x_3 = 3 + 2t
where t is a parameter and can be any number.
a) How many pivots are in the row echelon form of A?
b) Let u, v, w be the columns of A. Do they span the whole R^4? Explain.
c) Is u, v, w a linearly independent set? Explain.
d) Produce a linear relation for u, v, w. ( Hint: what is the solution of the system Ax = 0 ?)
Homework Equations
The Attempt at a Solution
My original attempt I tried to solve for the parameter t in hopes that this would give me a coefficient matrix for x that I could substitute in the equation for x but I could not make this work. I also realized that the solution set is linearly dependent as one of the rows can be expressed as linear combinations of the other rows but I don't know if this is significant information for this problem.
My secondary attempt was to consider a system where the solution set in the form listed above was b, then A would be a 4x3 identity matrix. I then multiplied each side of the equation by the 4x3 Identity matrix but multiplying the equation by 1 was not leading me to the next path, and thus now I sit here in utter confusion trying to make sense of this problem and is making me question my confidence in my other solutions on the assignment
 .
.Note: I am having trouble mainly with formulating an expression or method to solve Part A, but I feel with a few minor hints after formulating Part A I can handle the question. Thanks for the help!