- #1
Ryry013
- 2
- 0
Here is a picture of the problem.
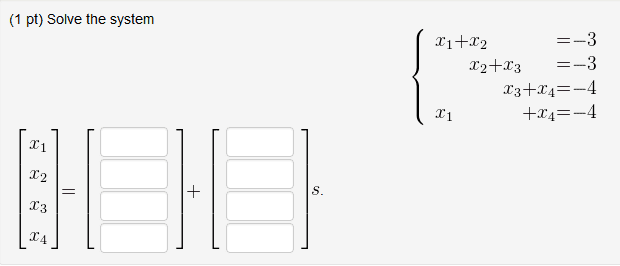 Can anyone give me some hints on the problem? I've looked in my textbook, but I don't know what "s" means. I found stuff on the parametric vector form, and it gives me the equation x = su + tv, but I don't see any "t"'s in this problem.
Can anyone give me some hints on the problem? I've looked in my textbook, but I don't know what "s" means. I found stuff on the parametric vector form, and it gives me the equation x = su + tv, but I don't see any "t"'s in this problem.
I first tried setting up an augmented matrix with
[ 1 1 0 0 | -3 ]
[ 0 1 1 0 | -3 ]
[ 0 0 1 1 | -4 ]
[ 1 0 0 1 | -4 ]
And I solved for the four variables, like:
x1 = -3 - x2
x2 = -3 - x3
x3 = -4 - x4
x4 = -4 - x1
And now I'm stumped. I didn't think these would do anything, but setting the first and second rows equal to each other, and the third and fourth rows equal to each other simply gets x1 - x3 = 0 for both of them.
I didn't think this would do anything either, but I tried also back substituting the x1 equation into the x4 equation, and then the x2 equation into x4, and so on, and that ended up with x4 = x4.
I first tried setting up an augmented matrix with
[ 1 1 0 0 | -3 ]
[ 0 1 1 0 | -3 ]
[ 0 0 1 1 | -4 ]
[ 1 0 0 1 | -4 ]
And I solved for the four variables, like:
x1 = -3 - x2
x2 = -3 - x3
x3 = -4 - x4
x4 = -4 - x1
And now I'm stumped. I didn't think these would do anything, but setting the first and second rows equal to each other, and the third and fourth rows equal to each other simply gets x1 - x3 = 0 for both of them.
I didn't think this would do anything either, but I tried also back substituting the x1 equation into the x4 equation, and then the x2 equation into x4, and so on, and that ended up with x4 = x4.