Linear expansion of steel versus copper with increasing temperature

[Eerik]

Homework Statement

Two engine components, made of steel and copper, are each 10 cm in length and are fixed so that they are only free to expend towards one another, so closing the gap between them as temperature rises. Calculate the clearance between them when the engine is at 15°C if there is to be a gap of 1 mm between them when the engine is at its running temperature of 150°C.

Linear expansivity of steel = 11 * 10^-6 per kelvin
Linear expansivity of copper = 17 * 10^-6 per kelvin

Relevant Equations

ẟL / Lo = α * ẟT
L = Lo (1+ α * ẟT)

ẟL = change in length
Lo = original length
L = new length
α = linear expansivity
ẟT = change in temperature

Here I'm going to show all that I've understood -
1.

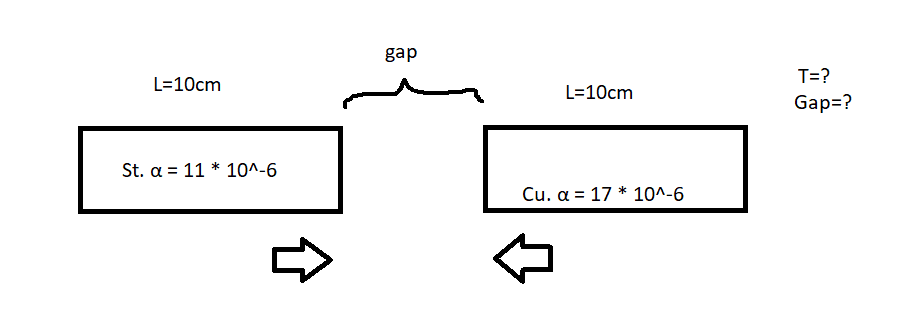
2.

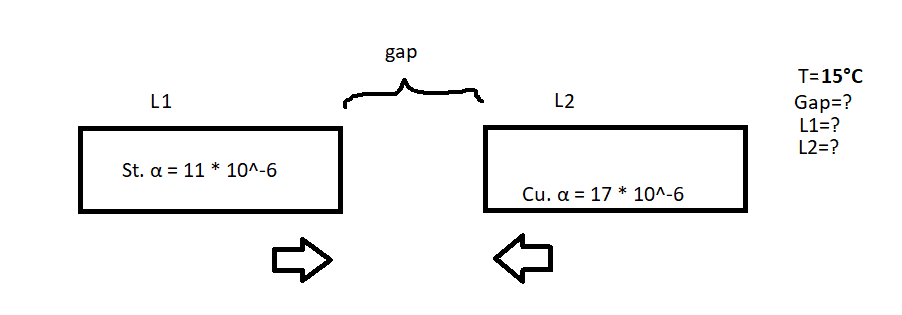
3.

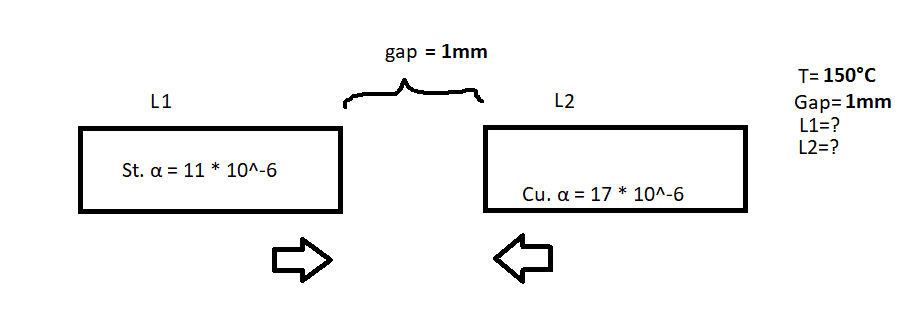
What I've attempted -

L = Lo (1+ α * ẟT)

ẟT = 150°C - 15°C = 135°C
(Steel) L = ẟL (1 + 11 * 10^-6 * 135)
(Copper) L = ẟL (1 + 17 * 10^-6 * 135)
This doesn't get me anywhere, obviously.

Am I supposed to understand from the task that the temperature is 15°C when the two engine components are 10cm length? Because then the task is rather simple. But I don't see it being implied in any way.

Thanks!

 

[mjc123]

Try it with L = 10 cm at 15°C, and again with L = 10 cm at 150°C. See if there is any significant difference in the answer.

 

[Chestermiller]

What I've attempted -

L = Lo (1+ α * ẟT)

This equation is correct. But it’s easier to write

$\delta L=L_0\alpha \delta T$

 

[onatirec]

My reading of the problem is that you should combine the first and second diagrams (known initial length + known initial temperature). Generally, with simple questions like this, you have all the information for one condition and partial information for another condition.