Linear motion converted into rotatory motion problem

[rabiakhan.91]

Homework Statement

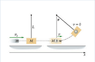
In a ballistic pendulum an object of mass m is fired with an initial speed v_0 at a pendulum bob. The bob has a mass M, which is suspended by a rod of length L and negligible mass. After the collision, the pendulum and object stick together and swing to a maximum angular displacement theta.
Find an expression for v_0, the initial speed of the fired object.
Express your answer in terms of some or all of the variables m, M, L, and theta and the acceleration due to gravity, g.
a figure is attached for better understanding!
please help! :(

Homework Equations

v= rω, s=rθ, ω=θ/t

The Attempt at a Solution

i have tried using the above examples but i don't know what to remove time since we are not asked to write in terms of time

 

[lewando]

Approach the problem from an energy and momentum point of view. Find final (maximum) PE, KE after the collision, KE before the collision.

 

[rabiakhan.91]

that was helpful! but while finding the potential energy, how will we find the height?

 

[Doc Al]

but while finding the potential energy, how will we find the height?

Use a bit of trig.

 

[rabiakhan.91]

i got the answer v = (2g(m+M)(L-Lcostheta)/m)^1/2
what do u think?

 

[Doc Al]

i got the answer v = (2g(m+M)(L-Lcostheta)/m)^1/2
what do u think?

Rather than just give your final answer, describe how you arrived at your answer.

 

[rabiakhan.91]

ok so i got the height as L-Lcostheta

the kinetic energy of the block is 0 and the kinetic energy of both of them at the heighest point is 0. so
1/2mv(initial)^2 = (m+M)g(L-Lcostheta)
then i just rearranged to find v

i am still a little doubtful about the height though

 

[Doc Al]

ok so i got the height as L-Lcostheta

the kinetic energy of the block is 0 and the kinetic energy of both of them at the heighest point is 0. so
1/2mv(initial)^2 = (m+M)g(L-Lcostheta)
then i just rearranged to find v

i am still a little doubtful about the height though

The height is just fine. But your assumption that energy is conserved during the collision is not.

 

[rabiakhan.91]

umm but then how will we find the equations?
K.E before the collision is 1/2mvinitial^2
after the collision = 1/2(m+M)v^2 + mg(L-Lcostheta)
momentum is conserved so
mvinitial = (m+M)v

 

[Doc Al]

momentum is conserved so
mvinitial = (m+M)v

Good. That's what you were missing.

Treat the motion as having two stages:
- The collision. Momentum (not energy) is conserved.
- The rise after the collision. Energy is conserved.

 

[rabiakhan.91]

so momentum is mvinitial = (m+M)v and after rearranging it will be v= mvinitial/(m+M)
then energy is conserved after collision 1/2(m+M)v^2 = mg(L-Lcosθ)

then we will substitute the value of v from the conservation of momentum equation so it will be
1/2 *mvinitial^2/(m+M) = g(L-Lcosθ)
and then rearranging, vinitial = 2g(m+M)(L-Lcosθ) / m

correct?

 

[lewando]

... energy is conserved after collision 1/2(m+M)v^2 = mg(L-Lcosθ)

The PE side of the equation's mass should be (m+M)

 

[rabiakhan.91]

o yes yes! sorry! so
the energy equation after substituting for v will be

[ (m+M) m^2 * vinitial ^2 ] /2(m+M) = (m + M)g (L-Lcostheta)

and then vinitial = [2g(m+M)^2 (L-Lcos theta)] ^1/2 / m

 

[lewando]

I didn't get that. Show all steps. At least show what you got for v.

 

[rabiakhan.91]

since momentum is conserved, collision before the moemntum is = after collision
mvinitial = (m+M)v
we rearrange for v so v= m vinitial/ (m+M)

then energy is conserved after the collision so

1/2 (m+M) v^2 = (m+M)g(L-Lcosθ)

then we replace v after collision with initial velocity so we substitute for it from the first equation in the second equation

1/2 (m +M) [m vinitial /(m+M) ] ^2 = (m+M)g (L-Lcosθ)
we simplify it and (m+M) is cancelled

so it becomes
1/2 * (m vinitial)^2 / (m+M) = (m+M) g(L-Lcosθ)

then rearrange (m vinitial)^2 = 2g(m+M)^2 (L-Lcosθ)
then take the square root of both the sides and send m to the other side
vinitial = [ 2g(m+M)^2 (L-Lcosθ) ] ^1/2 / m
vinitial = (m+M) [ 2g(L-Lcosθ ] ^1/2 /m

hope this clears up a little

 

[lewando]

Clears it up a lot. Good work by you!

 

[rabiakhan.91]

you have no idea how thankful i am of u!
u have helped me in return of no personal gain!
i am literally moved by your act of kindness!
thank you so so much!
hope all your problems(physics and otherwise :P) work out !


:)

 

[lewando]

You are welcome. You wish will be shared by me, Doc_Al, and many others.