Loading effect on Voltage Sources

[jegues]

Homework Statement

See figure.

Homework Equations

N/A.

The Attempt at a Solution

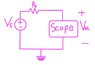
Okay first off I have a little confusion about the diagram in figure 3. Is Vnl simply the voltage across the oscilloscope in this figure? Is the circuit I've drawn in pink the same as figure 3?

I'm still confused how I can write Vnl in terms of Vs and Rs. Am I supposed to be using figure 3 or figure 4 to do this?
If I do infact have to use figure 4, Vo in the figure, is that suppose to be the same as Vnl?

If so then this is a simple voltage divider.

$$V_{o} = \frac{R_{L}}{R_{s} + R_{L}} \cdot V_{S}$$

Is this is what they are looking for?

The source of my confusion is in figure 3 they have Vnl on a point instead of being across an element (such as the scope), and how exactly I'm suppose to define Vnl using Vs and Rs.

Any tips/suggestions/comments would be greatly appreciated.

Thanks again!

EDIT: After doing some wiki reading on the loading effect, is it safe to assume that I can model my Oscilloscope in Figure 3 as a resistor Rscope and use that to define Vnl? The question asks what the value of Vnl is solely in terms of Vs, and Rs though... Is this possible?

If I can infact model my Oscilloscope as a resistor then Vnl would be expressed in terms of Vs, Rs and Rscope as follows,

$$V_{NL} = \frac{R_{scope}}{R_{scope} + R_{s}} \cdot V_{s}$$

 

[jegues]

Figured it out.

Since the scope's resistance is finitely high(but high enough), we can treat it as an open circuit.

KVL, no current flowing and VNL = Vs.