I'm bringing up again a discussion from which my participation was interrupted a while back when I lost my primary Internet access. I was going from dial-up to DSL, and ran into all kinds of mishaps, but that I'd rather not go into. The original problem statement went as follows:
vptran84 said:
Logic Function Using 74LS151
Hello all,
I'm having trouble with this certain problem...
Given: f(A,B,C,D) = AB'D' + B'C'D' + A'B'CD' + ACD + AB'C'D'
How do I build this logic function using one 74LS151 8-to-1 multiplexer and NAND gates?
Any help would be appreciate. I just need to be pointed in the right direction. THanks in advance.
Kenneth Mann said:
What you could do with it then is the following. Note that B' occurs that way in each term in which it appears. Thus you could use B' to enable the Multiplexer and just the four terms in which it is used to determine multiplexer inputs (ie. ACD => 000, 001 --- 110, 111). Use A, C, and D then to drive the mux (making sure that if A is the 'high order' bit in your table it is also used to drive the high order input to the mux. Thus, you'd have:
ACD' = 110
AC'D' = 100 (These first two make up the AB'D' term, with B' dropped)
AC'D' = 100
A'C'D' = 000 (these make up the B'C'D' term, notice the redundancy)
A'CD' = 010 (This makes up the A'B'CD' term)
AC'D' = 100 (This makes up the AB'C'D' term, again notice the redundancy)
Then for each of the values above, simply tie that (data) input to the multiplexer (there are four, the even values) up to Vcc (through a resistor; and ground the other four. Take the A, C and D lines also to a three-input NAND (in order to get the ACD term). Now, I am assuming the 74LS151 to have a 'non-inverting' output (I don't have the specs with me). If so, take the mux output along with the inversion of the B' input to another NAND; if not, leave it out. Finally, take the output from the mux, and from the just described NAND gate to another NAND.
Hope you can follow. Sorry I don't have the mux specs.
KM
Actually, this circuit could have tied either the first four inputs to Vcc, or the even inputs, etc. depending on how the ACD inputs are arranged. If the ACD inputs go in reverse order (DCA), what you would get is that shown in figure 3 of the accompanying attachments. This is the way I described them above. In hindsight I would have done it in forward order; it is a bit clearer.
chroot replied as follows:
chroot said:
KM,
Your solution, while perhaps workable, is not the simplest. All you need is a single two-input NAND and the 8-to-1 mux's inputs. You don't need to use enables or anything else.
- Warren
I agree now, that it isn't the simplest. The 'enable' input to the mux, however must be asserted. It cannot be left floating. The selected inputs also cannot be left to float.
Vptran84 did very well. He/(she?) began as follows:
vptran84 said:
i simplified the boolean equation and this is wat i got:
B'D' + ACD
is that correct?
On this, we all agree.
KM
chroot said:
vptran: yep, that's what I got too. Now, can you see an easy way to map that into the select pins of an 8-to-1 multiplexer?
- Warren
vptran84 said:
i drew up the truth table of the boolean equation and i got 1's at 0000, 0010, 1000, 1010, 1011, 1111.
So do i just put 1's at those numbers? and ground the rest?
chroot said:
Well, the 8-to-1 multiplexer only has three select bits -- it's not a 16-to-1. So you'll need to use a NAND gate to combine two of your inputs into one first.
- Warren
vptran84 said:
ok, so i used A C D as the inputs where A is the most significant bit. For B, i put it into a 2 input nand gate, which gives B' and connect that to Do, D2, D4, D6...for the rest, i grounded them. I guess it is becuase B is the one that controls the mux?? Can you tell me if I am on the rite track?
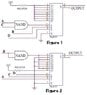
Actually, he could have done as he described, or he could have used D0, D1, D2 and D3, etc. depending on how the inputs are routed to the select logic. This circuit is shown in figure 2, and is the simplest of all. Note that the 'enable' input (G) must be selected by grounding it. ACD is selected by tying it to Vcc.
Kenneth Mann said:
You are good as far as you go, but what about the ACD case. You'll need one more wire for that. Also don't forget to ground the enable. This is a clever approach. The one I gave required two NANDs to handle the ACD case.
KM
chroot said:
As I've already said, use (AC)' as one of the select bits. Use B and D as the other two.
One NAND, one 8-to-1 mux, no need for enable logic.
The problem with the enable, Kenneth, is that it does not ground the outputs; it turns off the output drivers, putting them into the high-impedance (tri-state) state. You'd then have to add pull-up or pull-down resistors on the outputs. So now you're stuck with pull-up resistors and two NANDs, one of which is three-input -- a weird beast.
Basically, your solution is "clever" insofar as "clever" is a synonym for "pretty bizarre." There are better and cleaner ways to do it, as I have explained.
- Warren
In this case chroot is simply WRONG! First, the Enable input (G) to the mux
MUST be grounded. (All inputs must be asserted in some way.) Second, nobody said anything about grounding
OUTPUTs. Third, the output drivers to the 74LS151 are
NOT turned off. This is
NOT a Tri-state device. (Refer to the following:)
http://www.ee.washington.edu/stores/DataSheets/74ls/74ls151.pdf
http://grail.cba.csuohio.edu/~jackie/eces301/ds/sn74ls151rev5.pdf
The main problem, however, is chroot's use of the term "bizarre". That was unprofessional.
chroot said:
vptran:
As I've said, use (AC)', B, and D as the select inputs to your mux, and you're done.
- Warren
Actually, he's not done at that point. All of the data input lines (Ds) must also be tied (in this case to Vcc). Inputs can never be left to float. As it turns out, vptran's own solution was the best, but he was probably too intimidated to use it.
The three drawings in the accompanying attachment are used to illustrate the three approaches. Figure 1 shows the approach advocated by chroot, which I will admit is simpler than that of figure 3 (though I don't think that of figure 3 rises to the level of "bizarre"). Finally Figure 2 shows the approach put forth by vptran, which is the simplest (the best). (Note, that the NAND used could easily have been a simple inverter.)
Figure 4 is the statement of the original equation, which is mapped (one variation) in figure 6. From this map, the circuit in figure 3 can be readily defined. Figure 5 shows the equation partially simplified, which leads directly to the K-Map of figure 7. This can be readily translated into the circuit of figure 2.
It should be noted that a complete simplification of an equation gives a SSOP (Simple Sum of Products) or a SPOS Simple Product of Sums solution. These ore directly translatable to the use of NANDs or NORs. They do not readily yield answers for more complex devices, unless there is another step added, that of device-fitting, which can be quite complicated.
KM