Loop-de-loop work energy problem

[dorkymichelle]

Homework Statement

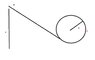
A particle of mass m slides along a frictionless track. It starts from rest at height h above the bottom of the loop of radius R.
A) what is the minimum value of h(in terms of R) such that the particle completes the loop? If the particle starts from height h=3.5R, find the force on the particle by the track. b) at the bottom of the loop c) at the point P, and d) at the top of the loop

Homework Equations

W= Kinetic final-kinetic initial
kinetic energy = 1/2mv^2
potential energy = mgh
Centripetal Acceleration = V^2/R

The Attempt at a Solution

So my thoughts on this so far is potential energy at bottom = kinetic energy before going into the loop. Energy required to go in the loop would > ... not sure what this is, but I know it has something to do with gravity, force of gravity?
/edit so I got a, the height which is 2.5R
but don't know how to do b where it asks for the force on the particle by the track.
all i got is
W=FdCostheta
W=1/2mv^2=Fdcostheta
mgh=Fdcostheta
what's the next step.
Not sure what theta would be at the bottom of the track.

 

[da_nang]

What is required for the particle to complete the loop? It has to reach the top of it with enough energy so as to continue forward. Now assume that it barely has enough energy for it. Then the energy at that point would basically be only potential energy. From there you can work out the minimum value of h in terms of R.

As for b), c) and d), you can use the conservation of energy to find the velocity at one point and use your knowledge of circular motion to calculate the net force on the particle. And don't forget gravity!