You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Lorentz Transformation of Fields
- Thread starter sampo
- Start date
Physics news on Phys.org
dextercioby
Science Advisor
- 13,389
- 4,044
Wow, a lot of to-the-point questions. I can't use the quote function to try to give an answer to each, because you inserted a picture. Indeed, Kaku's text does not fill in the gaps...
Do you know some group theory and representation theory, so that you'd be able to understand the answer ?
Do you know some group theory and representation theory, so that you'd be able to understand the answer ?
sampo
- 13
- 0
I can try. I know a little. Give me your best shot, thanks.
dextercioby
Science Advisor
- 13,389
- 4,044
So \epsilon_{\mu\nu} is a set of 6 independent infinitesimal parameters Kaku uses to describe the Lorentz group locally (i.e. in a neighborbood of the identity element). L^{\mu\nu} are then the generators of the connected component of the identity and can be taken as generators (basis elements) in the Lie algebra of the (restricted or full, doesn't matter) Lorentz group.
His first equation is axiomatic, it is the definition of the vector field in terms of its behavior under a restricted Lorentz transformation.
The explicit form of L's (with x and space-time derivatives) is valid in the case of scalar fields, because the spin of the field (angular momentum in the rest frame) is disregarded.
By physical reasons, U(\Lambda) is a unitary operator acting on the representation space of the restricted Lorentz group (actually a double cover of the restricted Poincare group), so by Stone's theorem, the L's should be (essentially) self-adjoint.
The calculation for the derivative of L(\Lambda) is wrong, as L depends on x and captures the implicit dependence of the U operator on x.
As for point 3), indeed, it's an Euler-MacLaurin series. Turns out that the epsilons are anti-symmetric.
Point 4) a) can be postulated (see above). b) Yes, all vectors have 4 space-time components. c) All fields, well, you move from the Lorentz group to the spin (1,3) group (SL(2,C)), so that spinorial fields will enter the picture.
This is off the top of my head. I can give you references such as Weinberg, Vol.1 or axiomatical field theory texts such as: Streater & Wightman (PCT, Spin-Statistics and All That) or better Bogolubov, Logunov, Todorov (1975 better than 1990).
His first equation is axiomatic, it is the definition of the vector field in terms of its behavior under a restricted Lorentz transformation.
The explicit form of L's (with x and space-time derivatives) is valid in the case of scalar fields, because the spin of the field (angular momentum in the rest frame) is disregarded.
By physical reasons, U(\Lambda) is a unitary operator acting on the representation space of the restricted Lorentz group (actually a double cover of the restricted Poincare group), so by Stone's theorem, the L's should be (essentially) self-adjoint.
The calculation for the derivative of L(\Lambda) is wrong, as L depends on x and captures the implicit dependence of the U operator on x.
As for point 3), indeed, it's an Euler-MacLaurin series. Turns out that the epsilons are anti-symmetric.
Point 4) a) can be postulated (see above). b) Yes, all vectors have 4 space-time components. c) All fields, well, you move from the Lorentz group to the spin (1,3) group (SL(2,C)), so that spinorial fields will enter the picture.
This is off the top of my head. I can give you references such as Weinberg, Vol.1 or axiomatical field theory texts such as: Streater & Wightman (PCT, Spin-Statistics and All That) or better Bogolubov, Logunov, Todorov (1975 better than 1990).
Last edited:
sampo
- 13
- 0
Excellent, thank you very much for the great reply. I am currently brushing up on my group theory. I imagine I will have a follow-up question, but while I continue to digest everything, I just wanted to say thanks!
I think one of my problems was how I was thinking of the Lorentz Group as a set of 4x4 matrices with real values, where I guess there is a representation in terms of the L operator. I estimate this is where my question will be, though I don't think I can formulate it yet.
I think one of my problems was how I was thinking of the Lorentz Group as a set of 4x4 matrices with real values, where I guess there is a representation in terms of the L operator. I estimate this is where my question will be, though I don't think I can formulate it yet.
dextercioby
Science Advisor
- 13,389
- 4,044
The Lorentz group IS (isomorphic to) a group of 4x4 matrices with real entries...
Hans de Vries
Science Advisor
Gold Member
- 1,094
- 31
L^{\mu\nu} contains the three generators of rotation J^i and the three generators of boosts K^i.
They form the Poincaré generators together with the four translation operators.
<br /> \begin{aligned}<br /> & P^\mu &=~& -i\Big( ~~~~~~~~~-\frac{\partial}{\partial x^\mu} &\Big)&<br /> ~~~\mbox{4 translation generators} \\<br /> & J^i &=~& -i\Big(\, ~~~~x^j\frac{\partial}{\partial x^k}-x^k\frac{\partial}{\partial x^j} &\Big)&<br /> ~~~\mbox{3 rotation generators}~~~~~~ \\<br /> & K^i &=~& -i\Big( ~ - x^i\frac{\partial}{\partial x^o}-x^o\frac{\partial}{\partial x^i} &\Big)&<br /> ~~~\mbox{3 boost generators}~~~~~~<br /> \end{aligned}<br />
In the image below you can see how they work. The \delta here is an infinitesimal small parameter.
You can for instance translate an arbitrary function over an infinitesimal small distance by
subtracting \delta\partial f/\partial x (The red and blue delta functions)
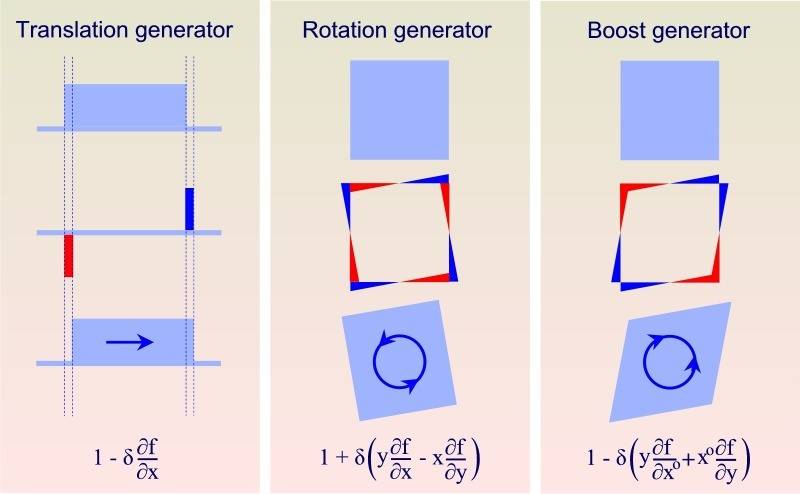
If you repeatedly apply the (1-\delta\partial_x f) operator then this amounts to an exponential function like
the one in your book. To translate over a distance \ell_x to the left you do:
<br /> \exp\left(\,i\ell_x P^x\right)\,f(x) ~=~<br /> \left\{1 +<br /> \frac{\ell_x }{1!}\,\frac{\partial }{dx } +<br /> \frac{\ell_x^2}{2!}\,\frac{\partial^2}{dx^2} +<br /> \frac{\ell_x^3}{3!}\,\frac{\partial^3}{dx^3} +<br /> \cdots\right\}f(x)<br />
The right hand side is just the standard Taylor series. If we write (x-a) for the displacement \ell_x and
let the operators act on f(a) then we get the familiar expression for the Taylor series.
<br /> f(a)+\frac {f'(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ \cdots<br />
The rotate and boost operators work in just the same way. The matrix \epsilon_{\mu\nu} contains the three angles
by which you want to rotate and the three rapidities by which you want to boost just like \ell_x is the
distance by which you want to translate.
The above rotates/boosts works on a scalar field, that is they handle the coordinate transformation.
If you want to transform a (four) vector field then have to operate on the (four) vector parameters
as well because the vector transforms under a general Lorentz transformation.
Hans
They form the Poincaré generators together with the four translation operators.
<br /> \begin{aligned}<br /> & P^\mu &=~& -i\Big( ~~~~~~~~~-\frac{\partial}{\partial x^\mu} &\Big)&<br /> ~~~\mbox{4 translation generators} \\<br /> & J^i &=~& -i\Big(\, ~~~~x^j\frac{\partial}{\partial x^k}-x^k\frac{\partial}{\partial x^j} &\Big)&<br /> ~~~\mbox{3 rotation generators}~~~~~~ \\<br /> & K^i &=~& -i\Big( ~ - x^i\frac{\partial}{\partial x^o}-x^o\frac{\partial}{\partial x^i} &\Big)&<br /> ~~~\mbox{3 boost generators}~~~~~~<br /> \end{aligned}<br />
In the image below you can see how they work. The \delta here is an infinitesimal small parameter.
You can for instance translate an arbitrary function over an infinitesimal small distance by
subtracting \delta\partial f/\partial x (The red and blue delta functions)
If you repeatedly apply the (1-\delta\partial_x f) operator then this amounts to an exponential function like
the one in your book. To translate over a distance \ell_x to the left you do:
<br /> \exp\left(\,i\ell_x P^x\right)\,f(x) ~=~<br /> \left\{1 +<br /> \frac{\ell_x }{1!}\,\frac{\partial }{dx } +<br /> \frac{\ell_x^2}{2!}\,\frac{\partial^2}{dx^2} +<br /> \frac{\ell_x^3}{3!}\,\frac{\partial^3}{dx^3} +<br /> \cdots\right\}f(x)<br />
The right hand side is just the standard Taylor series. If we write (x-a) for the displacement \ell_x and
let the operators act on f(a) then we get the familiar expression for the Taylor series.
<br /> f(a)+\frac {f'(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ \cdots<br />
The rotate and boost operators work in just the same way. The matrix \epsilon_{\mu\nu} contains the three angles
by which you want to rotate and the three rapidities by which you want to boost just like \ell_x is the
distance by which you want to translate.
The above rotates/boosts works on a scalar field, that is they handle the coordinate transformation.
If you want to transform a (four) vector field then have to operate on the (four) vector parameters
as well because the vector transforms under a general Lorentz transformation.
Hans
Last edited:
Similar threads
- Replies
- 31
- Views
- 5K
- Replies
- 3
- Views
- 3K
- Replies
- 2
- Views
- 1K
- Replies
- 11
- Views
- 1K
- Replies
- 3
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 11
- Views
- 1K
- Replies
- 2
- Views
- 8K
- Replies
- 7
- Views
- 1K
- Replies
- 1
- Views
- 3K
Hot Threads
-
I Please help me understand the double slit experiment and conclusion
- Started by jackjack2025
- Replies: 65
- Quantum Physics
-
B Can gravitons be detected?
- Started by Josiah
- Replies: 28
- Quantum Physics
-
I Qubit two-state quantum system
- Started by cianfa72
- Replies: 29
- Quantum Physics
-
I How to understand quantum computers?
- Started by Alex Notman
- Replies: 9
- Quantum Physics
-
B Yet another double slit thought experiment...
- Started by PhysicsIsReallyFun
- Replies: 20
- Quantum Physics
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math
