Magnetic field. I on understanding this problem.

[physics=world]

Homework Statement

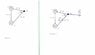
Two long parallel conductors carry currents I_1 = 3.0A and I_2 = 3.0A, both directed into the page. Find the magnitude and direction of the resultant magnitude field at point p?

Homework Equations

The Attempt at a Solution

I need help with this problem. The professor only provided the answer but not the steps. I'm having a hard time understanding what to do. I can do all the other problems, but when it comes to a problem like this (with having to apply vectors) I do not know what to do. Help me.

First I tried drawing the magnetic fields (figure 2). Then I found the angles - 23 degrees and 67 degrees.

I am stuck after this. How do I solve using vectors?

 

[Simon Bridge]

The total field is the vector sum of the individual fields - you know how to add vectors?

Anyway - did you draw the B vectors to be radial instead of tangential in there?
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html

Note - you have a special triangle there!
http://en.wikipedia.org/wiki/Special_right_triangles

 

[physics=world]

what do you mean by tangential?

 

[Simon Bridge]

The B field around a wire follows circles - at distance r, the B vector will be a tangent to the circle, centered on the wire, with radius r.

Is $\vec{B}_1$ the field due to $I_1$ and $\vec{B}_2$ the field due to $I_2$?
If so, they are pointing in the wrong directions. Please see the accompanying link.

 

[physics=world]

oh yes, I am sorry. your correct. i miswrote the B1 and B2.

 

[Simon Bridge]

OK - so... do you know how to add vectors?

 

[physics=world]

hmm is the special right triangle the triangle with the 90 degrees or is it the one with the added vectors?

 

[physics=world]

i know how to add vectors like moving head to tail, but not very well when it comes to the math.

 

[physics=world]

so at this point i would get a resultant vector that goes straight down. but I am confuse. do i do the x and y component for B1 and B2 separately or do i do the x and y component for the resultant component?

 

[Simon Bridge]

To use x-y components you need to define an x and y-axis - which is not provided for you.
Instead you should use the head-to-tail triangle of vectors and your knowledge of trigonometry.

One special triangle you have is the pythagorean triplet 5-12-13 ... point P is at the right angle.
It is probable that the B vectors also make two sides of a special triangle. They do conveniently make a right-angle with each other. If the resultant vector does go straight down, then it must be 5-12-13 as well.

There are lots of ways of specifying the direction of a vector.
If you label the position of I1 as Q and I2 and R, then the straight down direction is the Q-R direction ... or "parallel to $\overrightarrow{QR}$"