Magnetic field in the open loop

[tomfrank]

Homework Statement

I am trying to find the magnetic field at the point in the middle of the picture can someone give a hint on how to approach the problem?

Homework Equations

The Attempt at a Solution

 

[ApexOfDE]

Attachments Pending Approval...

 

[tomfrank]

any help?

 

[berkeman]

Homework Statement

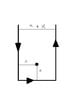
I am trying to find the magnetic field at the point in the middle of the picture can someone give a hint on how to approach the problem?

Homework Equations

The Attempt at a Solution

The hint is to use the Biot-Savart law... (Hint: it often simplifies the integration to make your variable of integration theta...)

 

[ApexOfDE]

you should divide the wire into some parts and find m.f created by these parts.

 

[tomfrank]

would the left and the right side cancel out...

So I have to do it just for the bottom side?

 

[tomfrank]

so thus this integral work :

B= (\mu*I)/(4*pi*x)\int between(-pi/4) and (pi/4) of cos (\theta) d\theta

 

[fluidistic]

would the left and the right side cancel out...

So I have to do it just for the bottom side?

I believe so (though I might be wrong). In all cases you should prove it via arithmetic so don't use this shortcut if you are not sure.

 

[ApexOfDE]

so thus this integral work :

B= (\mu*I)/(4*pi*x)\int between(-pi/4) and (pi/4) of cos (\theta) d\theta

No. Biot-Savart:

<br /> dB = \frac{\mu_0 I}{4 \pi} \frac{dl sin\theta}{r^2}<br />

With \theta is angle between dl and r. imo, you can use symmetry property to make life easier.

 

[tomfrank]

so i stil do not quite get it...does the two side cancel out?

<br /> <br /> dB = \frac{\mu_0 I}{4\pi r^2} {dl sin\theta}<br /> <br />

will the angle be (-pi/4) to (pi/4)

 

[ApexOfDE]

No. r is changing with theta. Can you find relationship between sin(theta) and r? and between r and x?

About two sides, you can say that they cancel out.

 

[tomfrank]

i see how you are looking at the picture.

basically the

sin (theta) dl = cos (theta') dl

and

1/r^2 = cos^2(theta')/ x^2
when i put all of them in the integral reduce down to

dB = \frac{\mu_0 I}{4\pi x} {dl cos\theta}<br /> <br />

i do not know yet what boundary to use for the integral

 

[ApexOfDE]

1/r^2 = cos^2(theta')/ x^2

from this, i guess theta and theta' as shown in fig below:

http://img149.imageshack.us/img149/6568/88285645.jpg

is that right?

 

[rl.bhat]

dB = μo/4π*I*di*sinθ/r^2
where sinθ = x/r = x/sqrt( x^2 + l^2)
Take the limits of integration from -x/2 to +x/2.

 

[tomfrank]

yes the picture with the angle is exactly what I was thinking...what are the limits for the integral angles?

 

[berkeman]

yes the picture with the angle is exactly what I was thinking...what are the limits for the integral angles?

The limits come from the geometry of the diagram. You really should be able to figure that part out.

And on your PM question to me, know, the B-field contributions from the two sides on the left and right do not cancel out.

 

[tomfrank]

i did to -45 to 45...will that work?

 

[berkeman]

i did to -45 to 45...will that work?

Based on your initial drawing, yes.

 

[tomfrank]

thank you