Magnetic Field of a Bent Wire: Point A & B Analysis

[stunner5000pt]

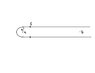
a long wire is bent into a hairpin as showqn in the figure. If the wire carries a current of i = 1.5A
a) what is the magnitude and the direction of B as point a?
b) at point b very far from a?
assume R = 5.2mm

a) for a
since R is constant s = 2 pi R
B = \frac{\mu_{0} i}{2R} and this field points straight out of the page.

b) for b the magnetic field is zero because the circular part has no effect on B. Also you have two wires carrying opposiute currents, thus creating equal and opposing fields thus the magnetic field is zero at B.

 

[mezarashi]

For part (a), I'm afraid the question may be a little more complicated. You will be looking at the Biot-Savart law.

In part (b), use the right hand rule. Do the fields cancel? If the current i is fluctuating, the magnetic field will fluctuate as well. Fluctuating magnetic fields introduce EMF. Why do you think wire pairs are usually twisted, and called twisted pairs as in CAT5 ethernet cables?

 

[stunner5000pt]

ok for the first part if I am using biot savart
B =\frac{\mu_{0} i}{4 \pi} \int \frac{ds \cross r}{r^3} then what is ds?
here ds seems to be infinitely long and the angle between ds and r varies from 180 to 90 and then from 90 to 180
then how would one find the relation between ds and theta?

 

[stunner5000pt]

also i is constant in the second part so there would be no emf created

we haven't gotten to that part of the chapter yet so I am thinking that would not be a factor here

ok due to the top part of the wire the field points upward
for the bottom part upward as well
so the field would be B = \frac{\mu_{0} i}{\pi R} ?

 

[mezarashi]

ds is your constant of integration of course. It is a differential element of your wire.

The correct form of the law is in fact.

B = \frac{\mu_o I}{4\pi}\int \frac{dl \times \vec{r}}{r^3}

If we want to solve without the use of vector calculus, we can simplify by deciding on the direction and working only with magnitudes. We can see that if the current and vector r is on the x-y plane, then the magnetic field must always be in the z or k direction. We can then write

B = \frac{\mu_o I}{4\pi}\int \frac{dl sin\theta}{r^2}

 

[mezarashi]

also i is constant in the second part so there would be no emf created
we haven't gotten to that part of the chapter yet so I am thinking that would not be a factor here

My example earlier was merely to show that the B field is indeed not zero. It is very real and also a problem in telecommunication systems.

ok due to the top part of the wire the field points upward
for the bottom part upward as well
so the field would be B = \frac{\mu_{0} i}{\pi R} ?

Yes, if you assume the infinite wire approximation where Ampere's law holds.

 

[stunner5000pt]

ds is your constant of integration of course. It is a differential element of your wire.

The correct form of the law is in fact.

B = \frac{\mu_o I}{4\pi}\int \frac{dl \times \vec{r}}{r^3}

If we want to solve without the use of vector calculus, we can simplify by deciding on the direction and working only with magnitudes. We can see that if the current and vector r is on the x-y plane, then the magnetic field must always be in the z or k direction. We can then write

B = \frac{\mu_o I}{4\pi}\int \frac{dl sin\theta}{r^2}

ok i get this so far
but isn't dl infinite? also doesn't theta vary?

 

[mezarashi]

ok i get this so far
but isn't dl infinite? also doesn't theta vary?

You need to apply your calculus. You cannot integrate unless your variable of integration is the same of that of the other variables present in the function. You have two choices, convert sin\theta into terms of length l or perform a change variables dl \longrightarrow d\theta. You will find that doing the latter will lead to a much much easier integral.

 

[stunner5000pt]

not sure how a change of variables would be used here...
i will attempt to find theta in terms of l
i use the attached diagram but perhaps i may not be doing this right

 

[mezarashi]

Change of variables starts by creating a relationship

tan \theta = \frac{d}{-l}
l = - d cot \theta
dl = d csc^2 \theta d\theta

Then your integral reduces to

B = \frac{\mu_o I}{4\pi}\int sin\theta d\theta

 

[stunner5000pt]

i see how that's done
you got a -l becuase of your refernce system
and theta varies from 180 to 90 and then 90 to 180 again

then the magnetic field would be \frac{\mu_{0} i}{2 \pi}
forh te semi cicular part of the loop
\frac{\mu_{0} i}{4R}
adding these two yields the magnetic field at a

 

[stunner5000pt]

one thing...
the magneticfield due to the top wire is integrated from theta = 180 to theta = 90
for the bottom one it is integrated from 90 to 180
when i subtract the two i get
\frac{\mu_{0} i }{2 \pi}


for the semio circular part the field is \frac{\mu_{0} i}{4R}
so the field at a is \frac{\mu_{0} i }{2 \pi} + \frac{\mu_{0} i}{4R}

is this correct/