boozi
- 7
- 0
Homework Statement
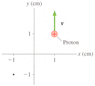
What are the magnetic field strength and direction at the dot in Figure Ex32.8, in which v = 3.0*10^7 m/s?
Figure Ex.32.8 is attached to the this post.
r = 0.02828 m
m0/4pi = 10^-7 T
v = 3.0*10^7 m/s
q = 1.60217653*10^-19 C
Homework Equations
Biot-Savart Law (attached), can't really type it...
The Attempt at a Solution
Ok. It's probably a very simple problem and it makes me feel really bad 'cause I can't solve it... I've tried to solve it with the Biot-Savart Law (check attach) with the values I mentioned above
I'm sure I calculated the cross product wrong.. How would I calculate it in this case? Thanks in advance.