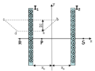pbstriker38
- 3
- 0
Two infinite sheets of current flow parallel to the y-z plane as shown. The sheets are equally spaced from the origin by xo = 7.5 cm. Each sheet consists of an infinite array of wires with a density n = 19 wires/cm. Each wire in the left sheet carries a current I1 = 3.5 A in the negative z-direction. Each wire in the right sheet carries a current I2 = 3.2 A in the positive z-direction.
What is
\int^b_aB⃗⋅dl⃗
where the integral is taken along the dotted line shown, from a to b.
2. Homework Equations
B = uI
B = 1/2 unI
3. The Attempt at a Solution
I used half of \intB⃗⋅dl⃗ for the closed loop abcd. Which resulted in "It looks like you've assumed that the integral of B dot dl from a to b is equal to 1/2 of the integral B dot dl around the closed path (abcda). That would be true, for example, if B dot dl at all points along the segment ab were equal to B dot dl at all points along the segment cd. This is not true here. The magnetic field along segment ab is not equal to the magnetic field along segment cd. Further, the orientation of B and dl are different in these two segments, as well. To answer this question, you actually have to do the integral of B dot dl from a to b. "
What is
\int^b_aB⃗⋅dl⃗
where the integral is taken along the dotted line shown, from a to b.
2. Homework Equations
B = uI
B = 1/2 unI
3. The Attempt at a Solution
I used half of \intB⃗⋅dl⃗ for the closed loop abcd. Which resulted in "It looks like you've assumed that the integral of B dot dl from a to b is equal to 1/2 of the integral B dot dl around the closed path (abcda). That would be true, for example, if B dot dl at all points along the segment ab were equal to B dot dl at all points along the segment cd. This is not true here. The magnetic field along segment ab is not equal to the magnetic field along segment cd. Further, the orientation of B and dl are different in these two segments, as well. To answer this question, you actually have to do the integral of B dot dl from a to b. "