besebenomo
- 11
- 1
- Homework Statement
- There is a circuit with resistance R, a moving bar of lenght l moves at constant velocity v=l/T and at t=0 the bar is in position x=0. In the beginning the circuit is in a region where B=0, the the bar starts moving into a region with a non-zero magnetic field (see figure), which varies with time.
What is the current flowing in the circuit?
- Relevant Equations
- Magnetic flux, Faraday's law
$$B(t) = B_{0} \frac{t^2}{T^2}$$
for ##0 \leq t \leq T##
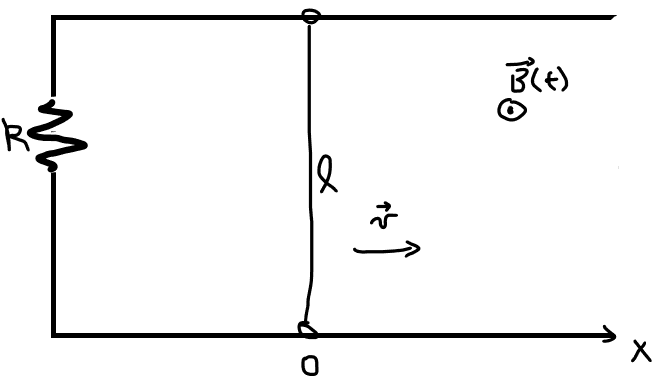
The issue here is more conceptual, because once I find the flux of B I know how to proceed to find the current. I got velocity (but it seems to me that it is the initial velocity), I could use it to find the time in function of space, but not sure if that is correct...
Instead I tried this way:
$$\Phi(B) = B_{0}\frac{t^2}{T^2} x(t)l$$
Should I integrate instead? And change variable?
for ##0 \leq t \leq T##
The issue here is more conceptual, because once I find the flux of B I know how to proceed to find the current. I got velocity (but it seems to me that it is the initial velocity), I could use it to find the time in function of space, but not sure if that is correct...
Instead I tried this way:
$$\Phi(B) = B_{0}\frac{t^2}{T^2} x(t)l$$
Should I integrate instead? And change variable?
Last edited: