Ignitia
- 21
- 5
Homework Statement
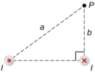
A circuit with current I has two long parallel wire sections that carry current in opposite directions. Find magneticfieldatapointPnearthesewiresthatisadistance a from one wire and b from the other wire as shown in the figure.
Homework Equations
B=μo*I / 2πR
The Attempt at a Solution
Field for I1:
B1 = μo*I / 2πb
Field for I1:
B2 = μo*I / 2πa
First have to calculate the x and y components:
Bnetx = B2 [ - sin(θ)] + B1 [cos(0)] = B2 [ - sin(θ)] + B1
Bnety = B2 [cos(θ)] + B1 [sin(0)] = B2 [cos(θ)]
cos(θ) = sqrt(a2 - b2) / a
sin(θ) = b/a
And find the total net value, Bnet = sqrt( Bnetx2 + Bnety2) so,
Bnet = sqrt( ( (μo*I / 2πa) [ - b/a] + (μo*I / 2πb))2 + (( μo*I / 2πa) [sqrt(a2 - b2) / a])2 )
And I just simplify this whole mess, correct? If it's correct up to here, then my mistake is only in the simplifying, and not the steps leading up to it.