TS656577
- 62
- 0
[SOLVED] Magnitude and acceleration
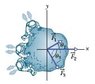
Three astronauts, propelled by jet backpacks, push and guide a 130 kg asteroid toward a processing dock, exerting the forces shown in the figure, with F1 = 32 N, F2 = 52 N, F3 = 39 N, θ1 = 30°, and θ3 = 60°. What is the (a) magnitude and (b) angle (measured relative to the positive direction of the x axis) of the asteroid's acceleration?
F=ma
If i had to make a guess...would i add the forces up which would be...129=ma where m is 130kg? Or would the magnitude be each mass squared and the square root of those sums which would be 72.45 in this case?
Homework Statement
Three astronauts, propelled by jet backpacks, push and guide a 130 kg asteroid toward a processing dock, exerting the forces shown in the figure, with F1 = 32 N, F2 = 52 N, F3 = 39 N, θ1 = 30°, and θ3 = 60°. What is the (a) magnitude and (b) angle (measured relative to the positive direction of the x axis) of the asteroid's acceleration?
Homework Equations
F=ma
The Attempt at a Solution
If i had to make a guess...would i add the forces up which would be...129=ma where m is 130kg? Or would the magnitude be each mass squared and the square root of those sums which would be 72.45 in this case?