bwilhelm
- 9
- 0
Homework Statement
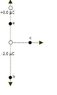
Two point charges are placed on the y-axis. One is +3.0 C and located at position (0, 2 m), the other is -2.0 C and located at the origin. Use the diagram to find the magnitude and direction of the electric field and the force on a +1.0 x 10-9 C test charge placed in the following locations.
a. (0, 1.0 m)
b. (0, -2.0 m)
c. (1.0m, 0)
Homework Equations
E= kq/(r^2)
The Attempt at a Solution
So for part a:
F= (K(3x10^-6)/(1^2) + K(2x10-6)/(1^2))
E= F/(test charge)
Same for part b, but the radius is different.
My question is how do I get part C?
I calculated the force between the -2uc charge and point C, but how do I get the force between the +3uc charge and point C?
Do I need to find the angle?