Magnitude of torque on a current loop

[ovoleg]

I've given this one a good effort and I cannot seem to solve it, been trying for a couple days on my own now...Anyone able to lend a hand?

I was using t=uxB(u cross B) to find the torque and then take the negative of it to find the torque that is to hold it?

vector u = I(vector A), and for this I am getting vector(A)=.0692i+.08j+.0346k
vector(B)=.58i+0j+0k
When I do the matrices for the cross(x) I get 0i+.321088j+.7424k

The only part of this that is right is the i component which is zero...

I'll be in your debt forever if you could help with a) or c)

Thanks!
------------------
The rectangular loop in Fig is pivoted about the y-axis and carries a current of 16.0 A in the direction indicated.((It's 16A, don't mind the picture saying 15A, this is the diagram below, click link))

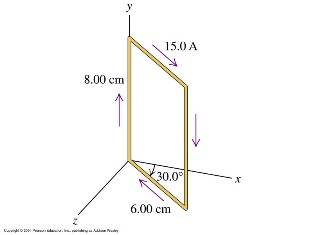a) If the loop is in a uniform magnetic field with magnitude 0.580 T in the +x-direction, find the magnitude and direction of the torque required to hold the loop in the position shown.
=

b) Repeat part (a) for the case in which the field is in the z-direction.
=

c) For each of the above magnetic fields, what torque would be required if the loop were pivoted about an axis through its center, parallel to the y-axis?
a =
b =

 

[andrewchang]

\tau = NIAB sin \Theta

N = number of loops
I = current
A = area of loop
B = magnetic field
theta = angle between loop and field

 

[ovoleg]

\tau = NIAB sin \Theta

N = number of loops
I = current
A = area of loop
B = magnetic field
theta = angle between loop and field

I love you! why doesn't my book have this?? :*(.

Thanks alot!

 

[electron]

well it is sinQ if we take the angle of rotatation in the geomtrical center of the loop...

just for information..heh